Bài 7 trang 71 Toán 8 Tập 2 Chân trời sáng tạo

Bài 7 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

Trong Hình 19, cho biết MN // BC, MB // AC.

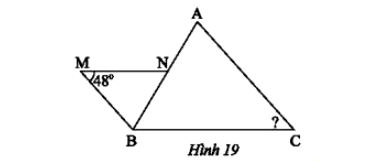
a) Chứng minh ΔBNM ᔕ ΔABC.

b) Tính ∠C

Phân Tích Hướng Dẫn Giải:

1. Đồng dạng (a): Hai tam giác đồng dạng (g.g) nếu hai cặp góc tương ứng bằng nhau. Ta sử dụng tính chất của góc so le trong và góc đồng vị tạo bởi các đường thẳng song song ($MN // BC$ và $MB // AC$).

2. Tính Góc (b): Vì hai tam giác đồng dạng, các góc tương ứng bằng nhau. Ta sẽ suy ra $\angle C = \angle N$. (Hoặc $\angle C = \angle M$ tùy theo thứ tự đồng dạng). Tuy nhiên, dựa trên việc so sánh các góc so le trong, ta cần xác định góc tương ứng với $\angle C$.

Giải bài 7 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔBNM và ΔABC ta có:

MN // BC nên $\widehat{MNB}=\widehat{ABC}$ (hai góc so le trong)

MB // AC nên $\widehat{MBN}=\widehat{BAC}$ (hai góc so le trong)

Vậy ΔBNM ᔕ ΔABC (g.g).

b) Do ΔBNM ᔕ ΔABC (cmt) nên $\widehat{C}=\widehat{B}=48^o$