Bài 9 trang 72 Toán 8 Tập 2 Chân trời sáng tạo

Bài 9 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

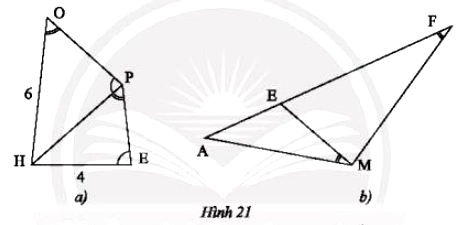
a) Trong Hình 21a, cho biết $\widehat{HOP}=\widehat{HPE}$, $\widehat{HPO}=\widehat{HEP}$, OH = 6 cm và HE = 4 cm. Tính độ dài đoạn thẳng HP.

b) Trong Hình 21b, cho biết  $\widehat{AME}=\widehat{AFM}$. Chứng minh rằng AM² = AE.AF.

Phân Tích Hướng Dẫn Giải:

1. Phần (a):

   • Chứng minh $\triangle HOP \sim \triangle HPE$ (g.g).

   • Thiết lập tỉ số đồng dạng sao cho cạnh $HP$ lặp lại (cạnh chung của hai tỉ số): $\frac{HO}{HP} = \frac{HP}{HE}$.

   • Giải phương trình $HP^2 = HO \cdot HE$.

2. Phần (b):

   • Chứng minh $\triangle AEM$ và $\triangle AMF$ đồng dạng theo trường hợp g.g.

   • Thiết lập tỉ số đồng dạng để cạnh $AM$ lặp lại: $\frac{AE}{AM} = \frac{AM}{AF}$.

   • Suy ra hệ thức $AM^2 = AE \cdot AF$.

Giải bài 9 trang 72 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔHOP và ΔHPE có: 

$\widehat{HOP}=\widehat{HPE}$ (gt)

$\widehat{HPO}=\widehat{HEP}$ (gt)

Nên ΔHOP ᔕ ΔHPE (g.g)

Suy ra $\frac{HO}{HP}=\frac{HP}{HE}$ (các cặp cạnh tương ứng).

Khi đó $\frac{6}{HP}=\frac{HP}{4}$ nên HP² = 6.4 = 24.

Vậy $HP=2\sqrt{6}\: (cm)$

b) Xét ΔAEM và ΔAMF ta có:

$\widehat{A}$ chung

$\widehat{AME}=\widehat{AFM}$

Nên ΔAEM ᔕ ΔAMF (g.g)

Suy ra  $\frac{AE}{AM}=\frac{AM}{AF}$ nên AM² = AE.AF (đpcm).