Bài 3 trang 70 Toán 8 Tập 2 Chân trời sáng tạo

Bài 3 trang 70 Toán 8 Tập 2 Chân trời sáng tạo: 

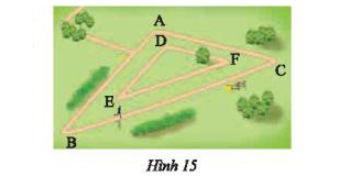
Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 660 m. Nam chạy bốn vòng trên con đường bên trong, Hùng chạy hai vòng trên con đường bên ngoài. So sánh quãng đường chạy được của hai bạn.

Phân Tích Hướng Dẫn Giải:

1. Tính tỉ số đồng dạng ($k$): Tỉ số $k$ bằng tỉ số giữa các cặp cạnh tương ứng. Cạnh ngắn nhất của đường bên trong ($300 \text{ m}$) phải tương ứng với cạnh ngắn nhất của đường bên ngoài ($660 \text{ m}$).

2. Tính độ dài đường chạy (Chu vi): Độ dài đường chạy chính là chu vi của tam giác. Tỉ số chu vi cũng bằng tỉ số đồng dạng $k$.

3. Tính tổng Quãng đường: Tính quãng đường chạy của Nam ($4 \times \text{Chu vi trong}$) và Hùng ($2 \times \text{Chu vi ngoài}$).

4. So sánh: So sánh hai kết quả quãng đường.

Giải bài 3 trang 70 Toán 8 Tập 2 Chân trời sáng tạo: 

Cạnh ngắn nhất của con đường bên ngoài là 600.m tương ứng với cạnh ngắn nhất của con đường bên trong là 300 m.

Do đó, con đường bên trong đồng dạng với con đường bên ngoài theo tỉ số:

$k=\frac{300}{600}=\frac{1}{2}$

nên tỉ số độ dài 2 con đường cũng bằng 1/2

Độ dài con đường bên trong là: 300 + 350 + 550 = 1200 (m).

Độ dài con đường bên ngoài: 2.1200 = 2400 (m)

Độ dài quãng đường Nam chạy: 4.1200 = 4800 (m).

Độ dài quãng đường Hùng chạy: 2.2400 = 4800 (m).

Vậy quãng đường chạy được của hai bạn bằng nhau.