Bài 5 trang 71 Toán 8 Tập 2 Chân trời sáng tạo

Bài 5 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

Trong Hình 17, cho biết DE = 6 cm, EF= 7,8 cm, NP = 13 cm, NM = 10 cm,  và . Tính 

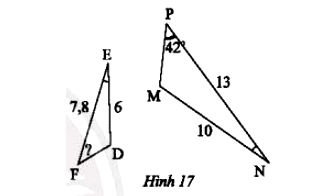
Phân Tích Hướng Dẫn Giải:

1. Xác định Đồng dạng (c.g.c): Kiểm tra xem hai tam giác $\triangle DEF$ và $\triangle MNP$ có đồng dạng hay không. Ta phải kiểm tra tỉ số của hai cặp cạnh kề với góc bằng nhau ($\widehat{E}$ và $\widehat{N}$).

   • Cặp cạnh kề $\widehat{E}$ là $DE$ và $EF$.

   • Cặp cạnh kề $\widehat{N}$ là $MN$ và $NP$.

2. Tính Góc: Nếu đồng dạng, các góc tương ứng bằng nhau. Ta sẽ suy ra $\widehat{F} = \widehat{P}$.

Giải bài 5 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

Xét ΔDEF và ΔMNP ta có:

$\frac{DE}{MN}=\frac{6}{10}=\frac{3}{5}$ và $\frac{EF}{NP}=\frac{7,8}{13}=\frac{3}{5}$

Suy ra: $\frac{DE}{MN}=\frac{EF}{NP}=\frac{3}{5}$

Mà $\widehat{E}=\widehat{N}$ (gt)

⇒ ΔDEF ᔕ ΔMNP (c.g.c)

Suy ra $\widehat{F}=\widehat{P}=42^o$ (hai góc tương ứng).

Vậy $\widehat{F}=42^o$