Bài 6 trang 71 Toán 8 Tập 2 Chân trời sáng tạo

Bài 6 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

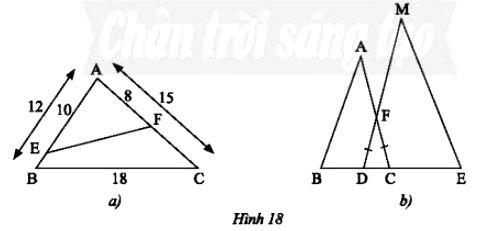
a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF.

b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABC ᔕ ΔMED.

Phân Tích Hướng Dẫn Giải:

1. Phần (a): Ta cần chứng minh $\triangle AFE \sim \triangle ACB$ (hoặc $\triangle AFE \sim \triangle ABC$). Sau đó, sử dụng tỉ số đồng dạng để tính cạnh $EF$.

2. Phần (b): Ta cần chứng minh $\triangle ABC$ và $\triangle MED$ đồng dạng theo trường hợp c.g.c. Phải kiểm tra tỉ số cạnh ($\frac{BC}{ED} = \frac{AC}{MD}$) và chứng minh góc xen giữa bằng nhau ($\widehat{C} = \widehat{D}$).

Giải bài 6 trang 71 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔAFE và ΔABC có:

$\frac{AF}{AB}=\frac{AE}{AC}=\frac{2}{3}$

$\widehat{A}$ chung

Nên ΔAFE ᔕ ΔABC (c.g.c)

Suy ra: $\frac{AF}{AB}=\frac{AE}{AC}=\frac{EF}{BC}$ (các cặp cạnh tương ứng).

Khi đó $\frac{8}{12}=\frac{10}{15}=\frac{EF}{18}=\frac{2}{3}$

Suy ra $EF=\frac{18.2}{3}=12\: (cm)$

Vậy EF = 12 cm.

b) Xét ΔABC và ΔMED ta có:

$\frac{BC}{ED}=\frac{AC}{MD}=\frac{3}{4}$

$\widehat{C}=\widehat{D}$ (tam giác FDC cân)

Vậy ΔABC ᔕ ΔMED (c.g.c).