Giải bài 10 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích...
Bài 10 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1): Cho tứ giác lồi ABCD có các đường chéo AC = x, BD = y và góc giữa AC và BD bằng α. Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh:
b) Nêu kết quả trong trường hợp AC ⊥ BD.
Giải bài 10 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1):
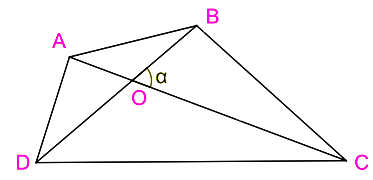
Gọi O là giao điểm của AC và BD
a) Chứng minh:
Áp dụng công thức:
Mà: sin(1800 - α) = sinα
Suy ra:
Lại có: SABCD = (SOAD + SOAB) + (SOBC + SOCD)
Vậy diện tích của tứ giác ABCD:
b) Trong trường hợp AC ⊥ BD.
Thì α = 900 ⇒ sinα = 1
Suy ra:
Hy vọng với lời giải bài 10 trang 73 Toán 10 Chân trời Sáng tạo (SGK Tập 1) ở trên đã giúp các em hiểu và nắm vững phần kiến thức này. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem giải bài tập Toán 10 Chân trời sáng tạo SGK tập 1 cùng chuyên mục
Đánh giá & nhận xét
-
 Biến cố là gì, biến cố chắc chắn và biến cố không thể, phép thử và không gian mẫu? Toán 10 chân trời tập 2 chương 10 bài 1
Biến cố là gì, biến cố chắc chắn và biến cố không thể, phép thử và không gian mẫu? Toán 10 chân trời tập 2 chương 10 bài 1
-
 Giải Bài tập Toán 10 tập 1 SGK Chân trời sáng tạo
Giải Bài tập Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 8 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 7 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 7 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 6 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 6 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 5 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 5 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 4 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 4 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 3 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 3 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 2 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 2 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 1 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 1 trang 93 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 5 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 5 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 4 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 4 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 3 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 3 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 2 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 2 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 1 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
Giải bài 1 trang 86 Toán 10 Chân trời sáng tạo SGK Tập 1
-
 Giải bài 6 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 6 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 78 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 77 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 9 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 9 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 8 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 8 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 7 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 7 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 6 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 6 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 73 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 72 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 7 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 7 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 6 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 6 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 65 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 9 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 9 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 8 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 8 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)


















































