Bài 8 trang 38 Toán 12 tập 1 Chân trời sáng tạo

Đề bài:

Cho hàm số 

Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên (-∞; -4) và nghịch biến trên (-4; +∞)

B. Hàm số đồng biến trên (-∞; 4) và (4; +∞) 

C. Hàm số nghịch biến trên (-∞; 4) và (4; +∞)

D. Hàm số nghịch biến trên (-∞; -4) và (-4; +∞)

Phân tích và Hướng dẫn giải

Để xét tính đơn điệu của hàm số, chúng ta cần tìm đạo hàm của hàm số đó.

• Hàm số phân thức bậc nhất:

• Đạo hàm: 

• Tập xác định: 

• Sau khi tính đạo hàm, ta dựa vào dấu của $y'$ để kết luận:

• Nếu  trên một khoảng, hàm số đồng biến trên khoảng đó.

• Nếu  trên một khoảng, hàm số nghịch biến trên khoảng đó.

Với bài toán này, ta sẽ tính đạo hàm, sau đó lập bảng biến thiên để có cái nhìn tổng quan nhất về sự đồng biến và nghịch biến của hàm số.

Lời giải chi tiết:

Đáp án: C. Hàm số nghịch biến trên (-∞; 4) và (4; +∞)

Ta có: TXĐ: D = R\{4}

Hàm số nghịch biến vợi mọi x ∈ D

Bảng biến thiên:

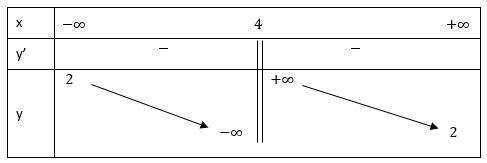
Từ bảng biến thiên, ta thấy: Hàm số nghịch biến trên (-∞; 4) và (4; +∞)