Bài 6 trang 14 Toán 12 tập 1 Cánh Diều

Đề bài:

Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T được tính bởi công thức sau:

V(T) = 999,87 - 0,06426T + 0,0085043T² - 0,0000679T³ 

Hỏi thể tích , giảm trong khoảng nhiệt độ nào?

Phân tích và hướng dẫn giải

Để xác định thể tích giảm, chúng ta cần tìm khoảng mà hàm số $V(T)$ nghịch biến. Theo kiến thức đã học, một hàm số nghịch biến khi đạo hàm của nó mang dấu âm. Các bước giải cụ thể:

1. Tìm tập xác định của hàm số $V(T)$.

2. Tính đạo hàm V′(T).

3. Tìm các giá trị của $T$ làm cho V′(T)=0.

4. Lập bảng biến thiên để xét dấu của V′(T) trên các khoảng.

5. Kết luận khoảng nhiệt độ mà tại đó V′(T)<0.

Lời giải chi tiết:

Tập xác định: D = R

Ta có: V'(T) = -0,06426 + 0,0170086T - 0,0002037T²

V'(T) = 0 ⇔ T ≈ 79,5 hoặc T ≈ 3,97

Bảng biến thiên:

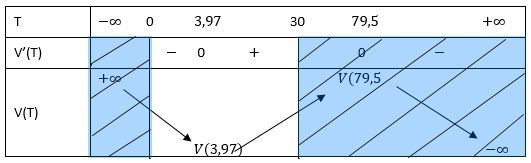
Vậy thể tích giảm trong khoảng nhiệt độ từ (0^o; 3,97^o).