Bài 5 trang 14 Toán 12 tập 1 Cánh Diều

Đề bài:

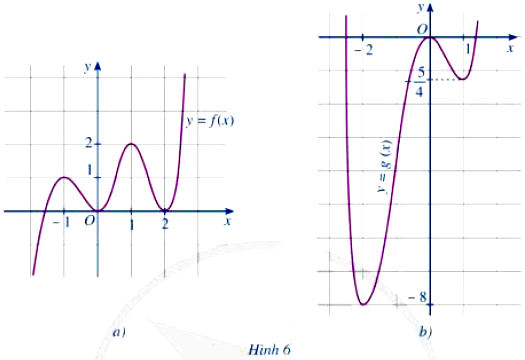
Cho hai hàm số y = f(x), y = g(x) có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.

Phương pháp phân tích đồ thị

Để phân tích đồ thị hàm số, các em hãy nhớ những nguyên tắc sau:

• Hàm số đồng biến: Đồ thị đi lên từ trái sang phải.

• Hàm số nghịch biến: Đồ thị đi xuống từ trái sang phải.

• Điểm cực đại: Điểm cao nhất trong một khoảng nhất định của đồ thị (từ "đỉnh" đi xuống).

• Điểm cực tiểu: Điểm thấp nhất trong một khoảng nhất định của đồ thị (từ "đáy" đi lên).

Lời giải chi tiết:

a) Hàm số đồng biến trên khoảng (-∞; -1), (0; 1), (2; +∞)

và nghịch biến trên khoảng (-1; 0) và (1; 2)

Hàm số đạt cực đại tại x = -1 và x = 1. 

Hàm số đạt cực tiểu tại x = 0 và x = 2

b) Hàm số đồng biến trên khoảng (-2; 0) và (1; +∞)

và nghịch biến trên khoảng (-∞; -2) và (0; 1)

Hàm số đạt cực đại tại x = 0.

Hàm số đạt cực tiểu tại x = 1 và x = -2.