Bài 4 trang 13 Toán 12 tập 1 Cánh Diều

Đề bài:

Tìm cực trị của mỗi hàm số sau:

a) y = 2x³ + 3x² - 36x - 10

b) y = x⁴ + 2x² - 3

c) 

Phân tích và hướng dẫn giải

Để tìm các điểm cực trị của hàm số, chúng ta thực hiện các bước sau:

1. Tìm tập xác định của hàm số.

2. Tính đạo hàm y′.

3. Giải phương trình y′=0 để tìm các nghiệm.

4. Lập bảng biến thiên và xét dấu của y′.

5. Dựa vào dấu của y′ để kết luận các điểm cực trị:

   • Cực đại: y′ đổi dấu từ dương sang âm khi đi qua điểm đó.

   • Cực tiểu: y′ đổi dấu từ âm sang dương khi đi qua điểm đó.

Lời giải chi tiết:

a) y = 2x³ + 3x² - 36x - 10

TXĐ: D = R

Ta có: y' = 6x² + 6x - 36 = 0 ⇔ x = 2 hoặc x = 3

Bảng biến thiên:

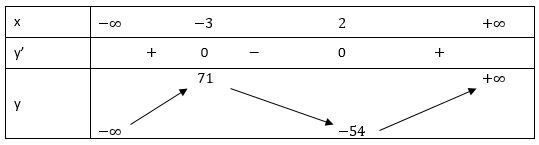
Vậy hàm số đạt cực đại tại điểm x = -3, y_CĐ = 71

và đạt cực tiểu tại x = 2, y_CT = -54

b) y = x⁴ + 2x² - 3

TXĐ: D = R

Ta có: y' = 4x³ + 4x = 0 ⇔ x = 0

Bảng biến thiên:

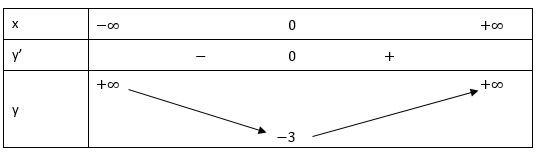
Vậy hàm số đạt cực tiểu tại x = 0, y_CT = -3

c) 

TXĐ: D = R\{0}

Ta có: 

Bảng biến thiên:

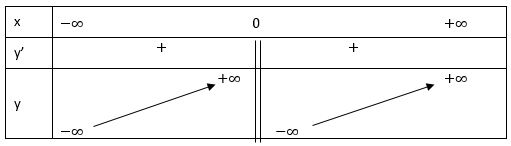Vậy hàm số không có điểm cực tiểu và điểm cực đại.