Bài 3 trang 13 Toán 12 tập 1 Cánh Diều

Đề bài:

Tìm các khoảng đơn điệu của hàm số sau:

a)  y = x³ + 2x² - 3

b) y = x⁴ - 2x² + 5

c) 

d)

Phân tích và Hướng dẫn giải

Để tìm các khoảng đơn điệu của một hàm số, chúng ta thực hiện các bước sau:

1. Tìm tập xác định của hàm số.

2. Tính đạo hàm y′.

3. Tìm các điểm mà tại đó y′=0 hoặc y′ không xác định. Đây là các điểm tới hạn.

4. Lập bảng biến thiên, xét dấu của y′ trên các khoảng xác định.

5. Dựa vào dấu của y′ để kết luận các khoảng đồng biến và nghịch biến:

   • Hàm số đồng biến khi y′>0.

   • Hàm số nghịch biến khi y′<0.

Lời giải chi tiết:

a)  y = x³ + 2x² - 3

TXĐ: D = R

Ta có: y' = 3x² + 4x = 0 ⇔ x = 0 hoặc x = 4/3

Bảng biến thiên:

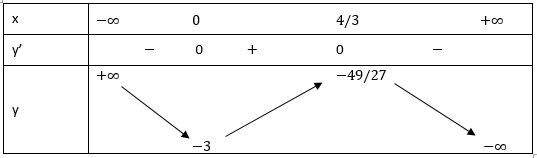
Vậy hàm số đồng biến trên khoảng (0; 4/3) 

Hàm số nghịch biến trên khoảng (-∞; 0) và (4/3; +∞)

b) y = x⁴ - 2x² + 5

TXĐ: D = R

Ta có: y' = 4x³ - 4x = 0 ⇔ x = 0 hoặc x = 1 hoặc x = -1

Bảng biến thiên:

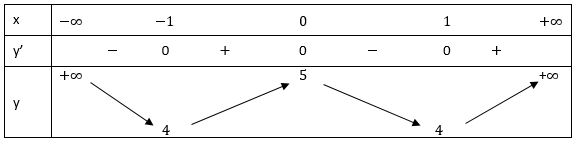
Vậy hàm số đồng biến trên khoảng (-1; 0) và (1; +∞) 

Hàm số nghịch biến trên khoảng (-∞; -1) và (0; 1)

c) 

TXĐ: D = R\{2}

Ta có: 

Bảng biến thiên:

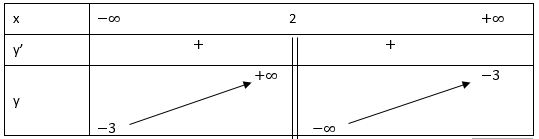
Vậy hàm số đồng biến trên khoảng (-∞; 2) và (2; +∞) 

d) 

TXĐ: D = R\{-1}

Ta có: 

Bảng biến thiên:

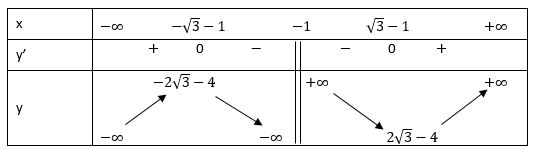
Vậy hàm số đồng biến trên khoảng (-∞; -1 - √3) và (-1 + √3; +∞) 

Hàm số nghịch biến trên khoảng (-1 - √3; -1) và (-1; -1 + √3)