Bài 7 trang 14 Toán 12 tập 1 Cánh Diều

Đề bài:

Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau:

v(t) = 0,001302t³ - 0,09029t² + 23

(v được tính bằng ft/s, 1 feet = 0,3048 m)

Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?

Phân tích và hướng dẫn giải

Để giải bài toán này, chúng ta cần nhớ mối quan hệ giữa vận tốc và gia tốc:

• Gia tốc là đạo hàm của vận tốc theo thời gian, tức là a(t)=v′(t).

• Để tìm khoảng thời gian mà gia tốc tăng, chúng ta cần tìm khoảng mà hàm gia tốc $a(t)$ đồng biến. Điều này xảy ra khi đạo hàm của gia tốc, tức là a′(t) (hay v′′(t)), mang dấu dương.

Các bước giải cụ thể:

1. Tính đạo hàm của hàm vận tốc $v(t)$ để tìm hàm gia tốc $a(t)$.

2. Tính đạo hàm của hàm gia tốc $a(t)$ để tìm a′(t).

3. Tìm các giá trị của $t$ làm cho a′(t)=0.

4. Lập bảng biến thiên để xét dấu của a′(t) trên các khoảng, trong đó thời gian được xét từ $t=0$ đến $t=126$.

5. Kết luận khoảng thời gian mà tại đó a′(t)>0.

Lời giải chi tiết:

Tập xác định: D = R

Ta có: v'(t) = 0,003906t² - 0,18058t

a(t) = v'(t) = 0 ⇔ t = 0 hoặc t ≈ 45,6

Bảng biến thiên:

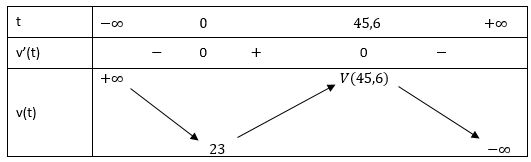
Vậy gia tốc tàu con thoi tăng trong khoảng 45,6s đầu tiên.