Bài 4 trang 57 Toán 12 tập 1 Chân trời sáng tạo

Đề bài:

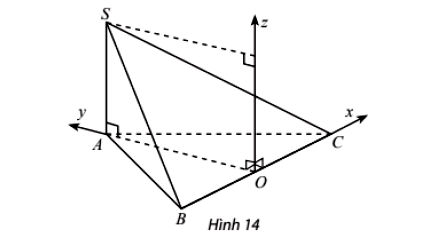
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1 (hình 14). Thiết lập hệ tọa đô như hình vẽ, hãy vẽ các vectơ đơn vị trên trục Ox, Oy, Oz và tìm tọa độ các điểm A, B, C, S.

Phân tích và Hướng dẫn giải:

Đề bài cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1. Chúng ta cần thiết lập một hệ trục tọa độ và tìm tọa độ của các điểm A, B, C, S.

Mấu chốt của bài toán là chọn hệ trục tọa độ một cách hợp lý để việc tính toán trở nên đơn giản. Dựa vào hình vẽ, ta thấy hệ trục đã được đặt sao cho gốc tọa độ O là trung điểm của BC, trục Oy đi qua A và trục Oz song song với SA.

Các bước thực hiện:

1. Xác định hệ trục tọa độ: Dựa vào hình vẽ, xác định gốc tọa độ và các trục tọa độ.

2. Tính toán các khoảng cách: Sử dụng các tính chất của tam giác đều và hình học phẳng để tính độ dài các đoạn thẳng cần thiết.

3. Tìm tọa độ các điểm: Dựa vào hệ trục tọa độ đã chọn và các khoảng cách đã tính, xác định tọa độ của từng điểm.

Lời giải chi tiết:

1. Xác định hệ trục tọa độ

Dựa vào hình vẽ, ta chọn hệ trục tọa độ Oxyz như sau:

• Gốc tọa độ O là trung điểm của cạnh BC.

• Trục Ox trùng với đường thẳng OC.

• Trục Oy trùng với đường thẳng OA.

• Trục Oz vuông góc với mặt phẳng (ABC) tại O và song song với SA.

Các vector đơn vị trên các trục Ox, Oy, Oz lần lượt là .

2. Tìm tọa độ các điểm A, B, C, S

Ta có tam giác ABC là tam giác đều cạnh 2. Vì O là trung điểm của BC, nên:

• 

• AO là đường cao của tam giác đều, nên 

  (a là độ dài cạnh tam giác đều).

Bây giờ, ta tìm tọa độ các điểm:

• Điểm O: Là gốc tọa độ, nên .

• Điểm B: Nằm trên trục Ox và cách O một khoảng 1 đơn vị theo chiều âm.

  Vậy, .

• Điểm C: Nằm trên trục Ox và cách O một khoảng 1 đơn vị theo chiều dương.

  Vậy, .

• Điểm A: Nằm trên trục Oy và cách O một khoảng  đơn vị.

  Vậy, .

• Điểm S: Vì SA song song với trục Oz, nên tọa độ S sẽ có cùng hoành độ và tung độ với A (hoặc O nếu ta coi SA là đường vuông góc hạ từ S xuống O, nhưng ở đây SA vuông góc với đáy tại A).

  SA vuông góc với mặt phẳng (ABC) tại A và SA = 1. Vậy S có tọa độ là . Tọa độ của A là . Chiều cao của hình chóp là SA = 1.

  Vậy,.