Giải bài 19 trang 110 SGK Toán 9 tập 1

Đề bài:

Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?

Phân tích và Hướng dẫn giải:

Để giải bài toán này, các bạn cần nắm vững định nghĩa và tính chất của đường thẳng tiếp xúc với đường tròn.

• Khoảng cách từ tâm đến đường thẳng: Kí hiệu là $d$. Khoảng cách này được tính bằng độ dài đoạn thẳng vuông góc kẻ từ tâm đến đường thẳng.

• Mối quan hệ tiếp xúc: Một đường thẳng được gọi là tiếp tuyến của một đường tròn khi và chỉ khi khoảng cách từ tâm đường tròn đến đường thẳng đó bằng bán kính ($d=R$).

Áp dụng tính chất này, chúng ta sẽ tìm ra tập hợp tất cả các điểm có thể là tâm của các đường tròn thỏa mãn yêu cầu của đề bài.

Lời giải chi tiết:

Ta có hình minh hoạ như sau: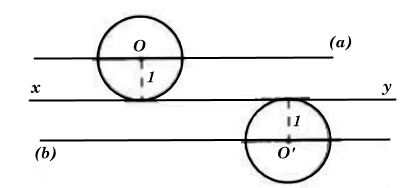

Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.

Ta có: R = 1, và đường tròn tiếp xúc với đường thẳng xy nên ta có: d = R ⇒ d = 1.

⇒ Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.