Bài 4.27 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài tập 4.27, trang 81 SGK Toán 9 Tập 1 (Kết nối tri thức), là bài toán ứng dụng tỉ số lượng giác vào mô hình thực tế (mái lều). Bài toán yêu cầu tính góc nghiêng $\alpha$ giữa mái lều và mặt đất, dựa trên chiều cao và độ rộng của đáy lều.
Bài 4.27 trang 81 Toán 9 Tập 1 Kết nối tri thức:
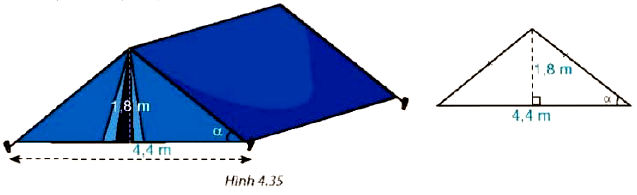
Hình 4.35 là mô hình của một túp lều. Tìm góc α giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
Phân Tích và Hướng Dẫn Giải:
-
Mô hình Tam giác vuông: Mô hình mái lều tạo thành một tam giác cân. Đường cao của lều ($1,8 \text{ m}$) chia tam giác cân này thành hai tam giác vuông bằng nhau. Góc $\alpha$ là một góc nhọn của tam giác vuông này.
-
Độ dài các cạnh:
-
Chiều cao (cạnh đối diện góc $\alpha$): $h = 1,8 \text{ m}$.
-
Cạnh kề góc $\alpha$: Bằng một nửa độ dài cạnh đáy: $k = \frac{4,4}{2} = 2,2 \text{ m}$.
-
-
Tỉ số Lượng giác: Ta có cạnh đối và cạnh kề của góc $\alpha$, nên ta sử dụng hàm tang ($\tan \alpha$).
$\mathbf{\tan \alpha = \frac{\text{Cạnh đối}}{\text{Cạnh kề}}}$
Giải bài 4.27 trang 81 Toán 9 Tập 1 Kết nối tri thức:
Ta có: $tan\alpha=\frac{1,8}{2,2}=\frac{9}{11}$
Suy ra α ≈ 39°17’.
Vậy góc α giữa cạnh mái lều và mặt đất là khoảng 39°17’.
Góc $\alpha$ giữa cạnh mái lều và mặt đất được xác định trong tam giác vuông bằng hàm $\tan \alpha = \frac{1,8}{2,2} = \frac{9}{11}$. Giá trị của góc $\alpha$, sau khi làm tròn đến phút, là $39^\circ 17'$.
» Xem thêm:
Bài 4.21 trang 81 Toán 9 Tập 1 Kết nối tri thức: Trong hình 4.32, cosα bằng...
Bài 4.25 trang 81 Toán 9 Tập 1 Kết nối tri thức: Giá trị tan30o bằng:...
Đánh giá & nhận xét
-
 Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.26 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.25 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.24 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.23 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.22 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
Bài 4.21 trang 81 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.23 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.27 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.26 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.25 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
Bài 3.24 trang 62 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
Bài 3.23 Toán 9 tập 1 SGK Kết nối tri thức
-
 Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.22 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.21 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.20 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.19 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.18 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
Bài 3.17 trang 59 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.16 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.15 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.14 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.13 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
Bài 3.12 trang 53 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.11 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.10 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.9 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.8 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
Bài 3.7 trang 51 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.6 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.5 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.4 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.3 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.2 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
Bài 3.1 trang 48 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.20 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.19 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.18 trang 41 Toán 9 tập 1 Kết nối tri thức
-
 Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn
Bài 2.17 trang 41 Toán 9 tập 1 Kết nối tri thức: Bất Phương Trình Bậc Nhất Một Ẩn
-
 Bài 2.16 trang 41 Toán 9 tập 1 Kết nối tri thức
Bài 2.16 trang 41 Toán 9 tập 1 Kết nối tri thức


















































