Cách giải phương trình chứa ẩn ở mẫu và bài tập vận dụng - Toán 8 chuyên đề (HayHocHoi Vn)
Là một trong những dạng toán về phương trình bậc nhất một ẩn, giải phương trình chứa ẩn là một trong những dạng bài tập làm khó nhiều em do kết luận nghiệm sai.
Vậy cách giải phương trình chứa ẩn ở mẫu như thế nào? cùng hay-học-hỏi.vn tìm hiểu qua bài viết dưới đây và vận dụng vào giải một số bài tập về phương trình chứa ẩn ở mẫu thức.
Các em hãy truy cập hoặc vào trang google tìm kiếm "tiêu đề bài viết" + "tên site
" để xem đầy đủ, chính xác và ủng hộ bài viết gốc của trang nhé. Vì hiện nay một số trang tự động sao chép lại, trình bày xấu, rất dễ thiếu sót làm các em khó hiểu.
» Đừng bỏ lỡ: Đầy đủ Các dạng toán về phương trình bậc nhất một ẩn và cách giải
• Cách giải phương trình chứa ẩn ở mẫu
- Phương trình có chứa ẩn ở mẫu là phương trình có dạng: 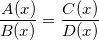
- Trong đó A(x), B(x), C(x), D(x) là các đa thức chứa biến x
Để giải phương trình ở mẫu các em thực hiện 4 bước sau:
- Bước 1: Tìm điều kiện xác định của phương trình.
- Bước 2: Qui đồng mẫu hai vế của phương trình, rồi khử mẫu.
- Bước 3: Giải phương trình vừa nhân được.
- Bước 4: (Kết luận) Trong các giá trị của ẩn tìm được ở bước 3, các giá trị thoả mãn điều kiện xác định chính là các nghiệm của phương trình đã cho.
* Ví dụ 1: Giải phương trình chứa ẩn ở mẫu sau:
* Lời giải:
Trước tiên ta tìm điều kiện xác định (ĐKXĐ) của phương trình
- ĐKXĐ: x ≠ 0 và 5x-1 ≠ 0 ⇔ x ≠ 0 và x ≠ 1/5;
- Ta có:
⇔ 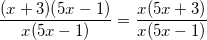
⇔ (5x - 1)(x + 3) = x(5x - 3)
⇔ 5x2 + 14x - 3 = 5x2 + 3x
⇔ 5x2 + 14x - 5x2 - 3x = 3
⇔ 11x = 3
⇔ x = 3/11 (thoả mã ĐKXĐ x ≠ 0 và x ≠ 1/5)
Vậy phương trình có tập nghiệm S = {3/11}.
* Ví dụ 2: Giải phương trình chứa ẩn ở mẫu sau: 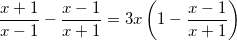
* Lời giải:
- ĐKXĐ của PT: x - 1 ≠ 0 và x + 1 ≠ 0 ⇒ x ≠ 1 và x ≠ -1
- Quy đồng và khử mẫu ta được:
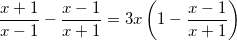
⇔ (x + 1)2 - (x - 1)2 = 3x(x - 1)(x+1 - x + 1)
⇔ x2 + 2x + 1 - x2 + 2x - 1 = 6x(x - 1)
⇔ 4x = 6x2 - 6x
⇔ 6x2 - 10x = 0
⇔ 2x(3x - 5) = 0
⇔ 2x = 0 hoặc 3x - 5 = 0
⇔ x = 0 hoặc x = 5/3 (thoả ĐKXĐ: x ≠ 1 và x ≠ -1)
Vậy tập nghiệp S = {0; 5/3}.
• Bài tập giải phương trình chứa ẩn ở mẫu
* Bài tập 1: Giải các phương trình chứa ẩn ở mẫu sau:
a) 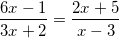
b) 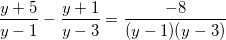
* Bài tập 2: Cho phương trình chứa ẩn x ở mẫu:
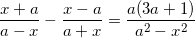
a) Giải phương trình với a = – 3.
b) Giải phương trình với a = 1.
c) Giải phương trình với a = 0.
* Bài tập 3: Giải phương trình chứa ẩn ở mẫu sau:
a)
b)
c)
Hy vọng với bài viết về Cách giải phương trình chứa ẩn ở mẫu và bài tập vận dụng Toán 8 ở trên giúp các em nắm vững kiến thức về phương trình bậc nhất. Mọi góp ý và thắc mắc các em hãy để lại phần bình luận dưới bài viết để Hay-Học-Hỏi.Vn ghi nhận và hỗ trợ, chúc các em học tập tốt
Đánh giá & nhận xét
-
 Cộng trừ phân thức cùng mẫu và khác mẫu, phân thức đối? Ví dụ? Toán 8 bài 2
Cộng trừ phân thức cùng mẫu và khác mẫu, phân thức đối? Ví dụ? Toán 8 bài 2
-
 Công thức tính thể tích, diện tích xung quanh hình chóp tam giác đều? Toán 8 bài 1
Công thức tính thể tích, diện tích xung quanh hình chóp tam giác đều? Toán 8 bài 1
-
 Cách nhân, chia hai phân thức đại số? phân thức nghịch đảo là gì? Ví dụ? Toán 8 bài 3
Cách nhân, chia hai phân thức đại số? phân thức nghịch đảo là gì? Ví dụ? Toán 8 bài 3
-
 Bảng giá trị và cách vẽ đồ thị của Hàm số bậc nhất y = ax + b? Toán 8 chân trời tập 2 chương 5 bài 3
Bảng giá trị và cách vẽ đồ thị của Hàm số bậc nhất y = ax + b? Toán 8 chân trời tập 2 chương 5 bài 3
-
 Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.33 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.33 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.32 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.32 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.31 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.31 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.30 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.30 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.29 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.29 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.18 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.18 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.17 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.17 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 11 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 11 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 10 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 10 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 9 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
Bài 9 trang 96 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 7 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 6 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 5 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 4 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 3 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 2 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
Bài 1 trang 95 Toán 8 Tập 2 Chân trời sáng tạo
-
 Bài 8.3 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.3 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.1 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.1 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.2 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.2 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.26 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.26 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.25 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.25 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.24 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.24 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.23 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.23 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.22 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.22 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.21 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.21 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.20 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.20 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.19 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.19 trang 76 Toán 8 Tập 2 Kết nối tri thức



















































