Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức

Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức:

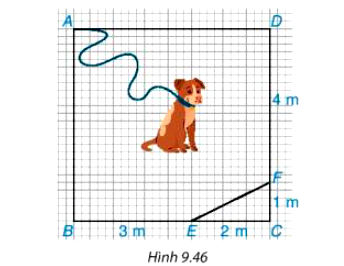
Chú cún bị xích bởi một sợi dây dài 6 m để canh một mảnh vườn giới hạn bởi các điểm A, B, E, F, D trong hình vuông ABCD có cạnh 5 m như Hình 9.44. Đầu xích buộc cố định tại điểm A của mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không?

Phân tích và Phương pháp giải

Điều kiện để chú cún đến được một điểm

Chú cún có thể di chuyển đến một điểm bất kỳ nếu và chỉ nếu khoảng cách từ điểm đó đến điểm buộc xích ($A$) nhỏ hơn hoặc bằng chiều dài sợi dây ($6$ m).

Các bước thực hiện

Ta cần kiểm tra khoảng cách từ $A$ đến các điểm xa nhất của mảnh vườn là $E, F$ và $C$ (mặc dù $C$ không nằm trong giới hạn trực tiếp nhưng nó là đỉnh xa nhất của hình vuông):

1. Tính AE: Sử dụng tam giác vuông $ABE$.

2. Tính AF: Sử dụng tam giác vuông $ADF$.

3. Tính AC: Sử dụng tam giác vuông $ADC$.

Giải Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức:

• Áp dụng định lí Pythagore cho tam giác ABE vuông tại B, có 

 AE² = AB² + BE² = 5² + 3² = 34.

⇒ AE = $\sqrt{34}$ m < 6 m.

Nên chú cún có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây.

• Áp dụng định lí Pythagore cho tam giác ADF vuông tại D, có 

 AF² = AD² + DF² = 5² + 4² = 41.

⇒ AF = $\sqrt{41}$ m > 6 m.

Nên chú cún không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây.

• Áp dụng định lí Pythagore cho tam giác ADC vuông tại D, có 

 AC² = AD² + DC² = 5² + 5² = 50.

⇒ AC = 5\sqrt{2} m > 6 m.

Nên chú cún không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây.

Vậy chú cún không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.