Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức

Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức:

Cho tam giác ABC cân tại đỉnh A, chiều cao AH = 3 cm và cạnh đáy BC = 10 cm. Hãy tính độ dài các cạnh bên AB, AC.

Phân tích và Phương pháp giải

Tính chất tam giác cân

Trong tam giác $ABC$ cân tại $A$, đường cao $AH$ hạ từ đỉnh $A$ xuống cạnh đáy $BC$ đồng thời là đường trung tuyến. Điều này có nghĩa là $H$ là trung điểm của $BC$, chia cạnh đáy thành hai đoạn thẳng bằng nhau: $HB = HC$.

Định lý Pythagore

Sau khi xác định được độ dài $HB$, ta sẽ xét tam giác vuông $AHB$ (vuông tại $H$). Áp dụng định lý Pythagore:

Từ đó, dễ dàng tính được độ dài cạnh bên $AB$ và suy ra $AC$.

Giải Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ sau:

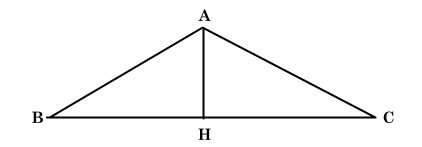
Vì tam giác ABC cân tại A có đường cao AH nên AH cũng là đường trung tuyến hay H là trung điểm BC.

⇒ HB = HC = BC : 2 = 10 : 2 = 5 cm.

Xét tam giác AHB vuông tại H, theo định lí Pythagore ta có

AB² = AH² + HB² = 3² + 5² = 34.

⇒ AB = $\sqrt{34}$ cm.

Do tam giác ABC cân tại A nên AC = AB = $\sqrt{34}$ (cm).