Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức

Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức:

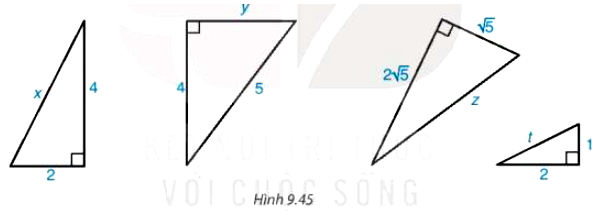
Tính độ dài x, y, z, t trong Hình 9.43.

Phân tích và Phương pháp giải

Kiến thức áp dụng

Toàn bộ các yêu cầu trong bài đều dựa trên Định lý Pythagore:

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

$c^2 = a^2 + b^2$ (với $c$ là cạnh huyền).

Chiến lược tính toán

• Tìm cạnh huyền: Nếu cần tính $x, z, t$ (đóng vai trò cạnh huyền), ta dùng công thức: $\text{Cạnh huyền} = \sqrt{\text{Tổng bình phương hai cạnh góc vuông}}$.

• Tìm cạnh góc vuông: Nếu cần tính $y$ (đóng vai trò cạnh góc vuông), ta dùng công thức: Cạnh góc vuông = Căn bạc 2 của (Bình phương cạnh huyền - Bình phương cạnh còn lại)

Giải Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức:

Vì các tam giác trong Hình 9.43 đều là các tam giác vuông nên ta áp dụng định lí Pythagore. Ta có:

• x² = 4² + 2² = 20 ⇒ x = $2\sqrt{5}$

• 5² = 4² + y² nên y² = 5² − 4² = 9 ⇒ y = 3.

• z² = $(\sqrt{5})^2+(2\sqrt{5})^2$ = 25 ⇒ z = 5.

• t² = 1² + 2² = 5 ⇒ t = $\sqrt{5}$