Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức

Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức:

Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ ΔHAN.

Phân tích và Hướng dẫn giải

• Mục tiêu: Chứng minh $\Delta HBM \sim \Delta HAN$.

• Dữ kiện: Tam giác $ABC$ vuông tại $A$, $AH \perp BC$, $M$ là trung điểm $AB$, $N$ là trung điểm $AC$.

• Hướng đi: 1. Đầu tiên, chứng minh hai tam giác vuông lớn là $\Delta HBA$ và $\Delta HAC$ đồng dạng.

  2. Từ tỉ số đồng dạng của hai tam giác lớn, kết hợp với giả thiết về trung điểm ($M, N$) để lập tỉ số cạnh cho hai tam giác con.

  3. Sử dụng trường hợp đồng dạng Cạnh - Góc - Cạnh (c.g.c).

Giải Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

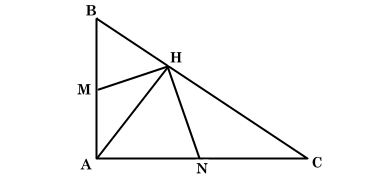
Vì tam giác ABC vuông tại A và tam giác HAC vuông tại H, nên có:

$\widehat{HBA}=\widehat{CBA}$ $=90^o-\widehat{ACB}=\widehat{HAC}$

Xét hai tam giác HBA vuông tại H và tam giác HAC vuông tại H có:

$\widehat{HBA}=\widehat{HAC}$ (chứng minh trên)

⇒ ∆HBA ∽ ∆HAC.

Suy ra: $\frac{HB}{HA}=\frac{BA}{AC}=\frac{2BM}{2AN}=\frac{BM}{AN}$ (Vì M, N là trung điểm của AB và AC).

Xét tam giác HBM và tam giác HAN có

$\frac{BM}{AN}= \frac{HB}{HA}$ (chứng minh trên)

$\widehat{HBA}=\widehat{HAC}$ hay $\widehat{HBM}=\widehat{HAN} $

⇒ ∆HBM ∽ ∆HAN (c.g.c).