Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức

Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức:

Trong Hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:

a) ΔAEH ∽ ΔAHB;

b) ΔAFH ∽ ΔAHC; 

c) ΔAFE ∽ ΔABC.

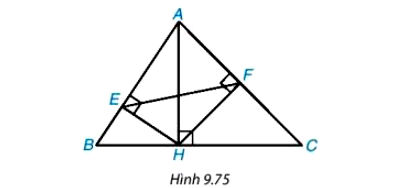
Phân tích và Hướng dẫn giải

• Câu a và b: Đây là dạng bài chứng minh tam giác vuông đồng dạng cơ bản. Chúng ta chỉ cần chỉ ra một góc nhọn chung giữa hai tam giác vuông đó.

• Câu c: Để chứng minh $\Delta AFE \sim \Delta ABC$, ta cần sử dụng kết quả từ câu a và b để thiết lập các tỉ số cạnh. Vì hai tam giác này có chung góc $A$, phương pháp khả thi nhất là chứng minh theo trường hợp Cạnh - Góc - Cạnh (c.g.c).

Giải Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức:

a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có:

Góc BAH chung.

⇒ ΔAEH ∽ ΔAHB.

b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có:

Góc CAH chung.

⇒ ΔAFH ∽ ΔAHC. 

c) Vì ΔAEH ∽ ΔAHB nên 

$\frac{AE}{AH}=\frac{AH}{AB}\Rightarrow AE=\frac{AH^2}{AB}$ (1)

Vì ΔAFH ∽ ΔAHC nên 

$\frac{AF}{AH}=\frac{AH}{AC}\Rightarrow AF=\frac{AH^2}{AC}$ (2)

Từ (1) và (2) ⇒ AE . AB = AF. AC

hay $\frac{AF}{AB}=\frac{AE}{AC}$

Tam giác AFE và tam giác ABC có:

$\widehat{BAC}$ chung; 

$\frac{AF}{AB}=\frac{AE}{AC}$

⇒ ΔAFE ∽ ΔABC (c.g.c).