Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức

Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức:

Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.

a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?

b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét? 

Phân tích và Hướng dẫn giải

Nguyên lý toán học: Tại cùng một thời điểm, các tia sáng mặt trời được xem là song song với nhau. Do đó, cột cờ và bóng của nó tạo thành một tam giác vuông đồng dạng với tam giác vuông tạo bởi bạn An và bóng của bạn ấy.

• Chiều cao vật thể và độ dài bóng là hai cạnh góc vuông.

• Tỉ số giữa chiều cao vật và độ dài bóng luôn không đổi tại một thời điểm nhất định.

Giải Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ sau:

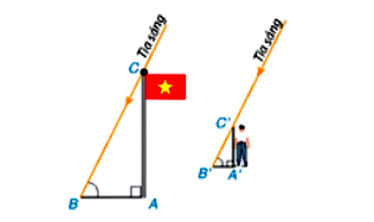
a) Ta có 60 cm = 0,6 m.

Vì tam giác vuông có hai cạnh góc vuông là cột cờ và bóng của cột cờ đồng dạng với tam giác vuông có hai cạnh góc vuông là An và bóng của An (do góc tạo bởi cạnh huyền với mỗi chiếc bóng trong mỗi tam giác là góc tạo bởi tia nắng với chiếc bóng và chúng xem như bằng nhau do mặt trời ở rất xa).

Vì vậy nếu gọi h là chiều cao cột cờ ta có:

$\frac{h}{1,4}=\frac{3}{0,6}$ suy ra $h=\frac{3.1,4}{0,6}=7(m)$

Vậy cột cờ cao 7 m.

b) Gọi k là chiều dài của bóng cột cờ vào lúc chiều, ta có:

$\frac{h}{1,4}=\frac{k}{3}$ suy ra $k=\frac{3.h}{1,4}=\frac{3.7}{1,4}=15(m)$

Vậy bóng cột cờ vào buổi chiều dài 15 m.