Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức

Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức:

Hãy tính diện tích của một hình chữ nhật có chiều rộng 8 cm và đường chéo dài 17 cm.

Phân tích và Phương pháp giải

Mối liên hệ giữa hình chữ nhật và tam giác vuông

Hình chữ nhật có 4 góc vuông. Khi vẽ một đường chéo, hình chữ nhật sẽ được chia thành hai tam giác vuông bằng nhau.

• Cạnh huyền: Chính là đường chéo của hình chữ nhật ($17$ cm).

• Hai cạnh góc vuông: Chính là chiều dài và chiều rộng của hình chữ nhật.

Các bước thực hiện

1. Sử dụng định lý Pythagore: Xét tam giác vuông tạo bởi đường chéo và hai cạnh để tìm chiều dài còn lại.

   $$a^2 + b^2 = c^2$$

2. Tính diện tích: Khi đã có đủ chiều dài và chiều rộng, áp dụng công thức:

   $$S = \text{Chiều dài} \times \text{Chiều rộng}$$

Giải Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

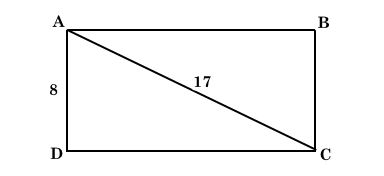
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta có:

AB² + BC² = AC².

⇒ BC² = AC² – AB² = 17² – 8² = 225.

⇒ BC = 15 (cm).

Vậy độ dài cạnh BC = 15 cm.

Diện tích của hình chữ nhật là: AB . BC = 8 . 15 = 120 (cm²).