Bài 7.17 trang 33 Toán 7 Tập 2 Kết nối tri thức
Bài tập 7.17, trang 33 SGK Toán 7 Tập 2 (Kết nối tri thức), là bài toán ứng dụng đa thức một biến trong hình học thực tế, cụ thể là tính diện tích của mảnh đất và bể bơi. Bài toán yêu cầu viết các biểu thức đa thức cho diện tích, bao gồm cả diện tích phần đất còn lại sau khi xây bể bơi.
Bài 7.17 Trang 33 Toán 7 Kết nối tri thức Tập 2:
Trên một mảnh đất hình chữ nhật có chiều dài 65 m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong Hình 7.1 Tìm đa thức (biến x):
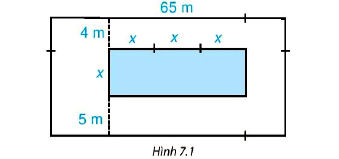
a) Biểu thị diện tích của bể bơi.
b) Biểu thị diện tích mảnh đất.
c) Biểu thị diện tích phần đất xung quanh bể bơi.
Phân tích Kích thước
-
Bể bơi:
-
Chiều rộng: $x \text{ m}$
-
Chiều dài: $3x \text{ m}$
-
-
Mảnh đất:
-
Chiều dài: $65 \text{ m}$ (Bằng chiều dài bể bơi + khoảng cách hai bên, theo sơ đồ)
-
Chiều rộng: $4 + x + 5 = x + 9 \text{ m}$
-
Giải Bài 7.17 Trang 33 Toán 7 Kết nối tri thức Tập 2:
a) Do chiều dài của bể bơi gấp 3 lần chiều rộng nên chiều dài của bể bơi là 3x m.
Diện tích của bể bơi là 3x.x = 3x2 (m2).
b) Chiều rộng của mảnh đất là: 4 + x + 5 = x + 9 (m).
Diện tích mảnh đất là: 65(x + 9) (m2).
c) Diện tích phần đất xung quanh bể bơi bằng diện tích mảnh đất trừ đi diện tích bể bơi.
Diện tích phần đất xung quanh bể bơi bằng:
65(x + 9) - 3x2 = 65x + 65.9 - 3x2 = -3x2 + 65x + 585 (m2).
Như vậy, ta có kết quả sau:
| Đại lượng | Đa thức biểu thị diện tích (m²) | Bậc của đa thức |
| a) Diện tích bể bơi | $\mathbf{3x^2}$ | 2 |
| b) Diện tích mảnh đất | $\mathbf{65x + 585}$ | 1 |
| c) Diện tích phần đất xung quanh | $\mathbf{-3x^2 + 65x + 585}$ | 2 |
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 9.9 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.9 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.8 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.8 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.7 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.7 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.6 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.6 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.35 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.35 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.34 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.34 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.33 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.33 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.32 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.32 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.31 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.31 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.30 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.30 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.29 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.29 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.28 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.28 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.27 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.27 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.26 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.26 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.25 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.25 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.24 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.24 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.23 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.23 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.22 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.22 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.21 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.21 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.20 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.20 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.19 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.19 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.18 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.18 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.17 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.17 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.16 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.16 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.15 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.15 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.14 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.14 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.13 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.13 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.12 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.12 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.11 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.11 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.10 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.10 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.7 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.7 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.6 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.6 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.5 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.5 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.4 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.4 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.15 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.15 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.14 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.14 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.13 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.13 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.12 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.12 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.11 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.11 SGK Toán 7 Tập 2 Kết nối tri thức


















































