Bài 9.32 trang 83 Toán 7 Tập 2 Kết nối tri thức

Bài 9.32 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Phân tích và Hướng dẫn giải

1. Phân tích giả thiết

• Ba điểm $A, B, C$ thẳng hàng $\Rightarrow$ $C$ nằm trên đường thẳng $AB$.

• $d \perp AB$ tại $A$, mà $M, N$ thuộc $d$ $\Rightarrow$ $NA \perp AC$ và $MA \perp AC$.

• $B$ nằm trên $AC$, nên $CA$ chính là đường cao hạ từ đỉnh $C$ của $\Delta MNC$.

• Đề bài cho $NB \perp MC$ $\Rightarrow$ $NB$ là đường cao thứ hai của $\Delta MNC$.

2. Hướng chứng minh

Để chứng minh $BM \perp CN$, ta cần chứng minh $BM$ là đường cao thứ ba của $\Delta MNC$. Cách đơn giản nhất là chứng minh điểm $B$ là trực tâm (giao điểm của các đường cao) trong tam giác $MNC$.

Giải bài 9.32 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Ta có hình minh họa như sau:

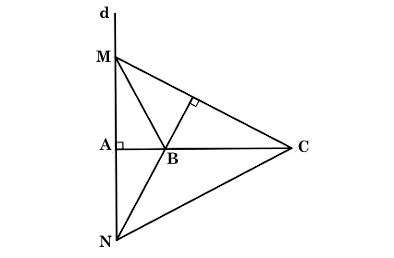
Xét ∆MNC có NB ⊥ MC, CB ⊥ MN.

Mà NB cắt CB tại B nên B là trực tâm của ∆MNC.

⇒ BM ⊥ CN (đpcm)