Bài 9.27 trang 81 Toán 7 Tập 2 Kết nối tri thức

Bài 9.27 Trang 81 Toán 7 Kết nối tri thức Tập 2: 

Cho tam giác ABC có ∠A = 100^o và trực tâm H. Tính góc BHC.

Phân tích và Phương pháp giải

Kiến thức áp dụng

• Trực tâm: Là giao điểm của ba đường cao trong tam giác.

• Tam giác vuông: Trong tam giác vuông, hai góc nhọn phụ nhau (tổng bằng $90^\circ$).

• Góc đối đỉnh: Hai góc đối đỉnh thì bằng nhau.

Chiến lược giải bài

Vì $\widehat{A} = 100^\circ$ (tam giác tù), trực tâm $H$ nằm ngoài tam giác. Ta sẽ sử dụng các tam giác vuông được tạo bởi các đường cao để thiết lập mối quan hệ giữa các góc tại đỉnh $A$ và góc tại trực tâm $H$.

Giải bài 9.27 Trang 81 Toán 7 Kết nối tri thức Tập 2: 

Ta có hình minh họa như sau:

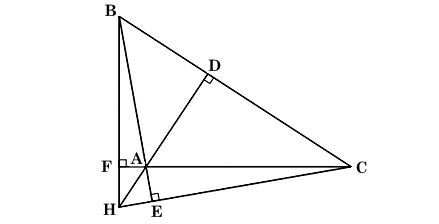
Gọi D, F, E lần lượt là chân đường cao kẻ từ A, B, C đến BC, CA, AB.

Ta có $\widehat{BAD}=\widehat{EAH}$ (2 góc đối đỉnh)

$\widehat{DAC}=\widehat{FAH}$ (2 góc đối đỉnh).

Do đó: $\widehat{BAD}+\widehat{DAC}$ $= \widehat{EAH}+\widehat{FAH}=100^o$

Xét ∆FAH vuông tại F: $\widehat{FHA}+\widehat{FAH}=90^o$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Suy ra: $\widehat{FHA}=90^o-\widehat{FAH}$

Xét ∆EAH vuông tại E: $\widehat{EHA}+\widehat{EAH}=90^o$ (trong tam giác vuông, hai góc nhọn phụ nhau).

Nên $\widehat{EHA}=90^o-\widehat{EAH}$

Khi đó: $\widehat{FHA}+\widehat{EAH}$ $=90^o-\widehat{FAH}+90^o-\widehat{EAH}$

Suy ra: $\widehat{BHC}=180^o-(\widehat{FAH}+\widehat{EAH})$

Suy ra: $\widehat{BHC}=180^o-100^o=80^o$

Vậy $\widehat{BHC}=80^o$