Bài 9.35 trang 83 Toán 7 Tập 2 Kết nối tri thức

Bài 9.35 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Kí hiệu S_ABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

a) Chứng minh S_GBC = S_ABC.

Gợi ý. Sử dụng GM = AM để chứng minh S_GBM = S_ABM, S_GCM = S_ACM.

b) Chứng minh S_GCA = S_GAB = S_ABC.

Nhận xét. Từ bài tập trên ta có: S_GBC = S_GCA = S_GAB = S_ABC điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.

Giải bài 9.35 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Ta có hình minh họa như sau:

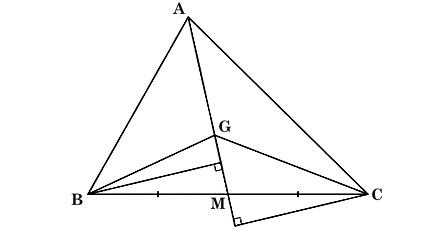
a) Do G là trọng tâm của tam giác ABC và M là trung điểm của BC nên GM = AM.

∆ABM và ∆MBG có chung đường cao kẻ từ B đến AM nên tỉ số diện tích giữa ∆MBG và ∆ABM bằng tỉ số của hai đáy GM và AM.

Ta có GM = AM nên S_MBG = S_ABM.

∆ABM và ∆MBG có chung đường cao kẻ từ C đến AM nên tỉ số diện tích giữa ∆MBG và ∆ABM bằng tỉ số của hai đáy GM và AM.

Ta có GM = AM nên S_MCG = S_ACM.

⇒ S_MBG + S_MCG = S_ABM + S_ACM

hay S_GBC = S_ABC.

b) Ta có AG = 2GM

Nên S_GCA = 2S_MCG; S_GAB = 2S_MBG.

Vì BC = 2MB = 2MC nên S_GBC = 2S_MCG = 2S_MBG.

⇒ S_GCA = S_GAB = S_GBC = S_ABC.