Bài 9.34 trang 83 Toán 7 Tập 2 Kết nối tri thức

Bài 9.34 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Phân tích và Hướng dẫn giải

Phân tích giả thiết và kết luận

• Giả thiết:

  • Gọi $Ax$ là tia đối của tia $AC$. Khi đó $\widehat{xAB}$ là góc ngoài tại đỉnh $A$ của tam giác $ABC$.

  • $At$ là tia phân giác của $\widehat{xAB}$ nên $\widehat{xAt} = \widehat{tAB}$.

  • $At \parallel BC$.

• Kết luận: Chứng minh $\Delta ABC$ cân tại $A$ (tức là chứng minh $\widehat{ABC} = \widehat{ACB}$).

• Hướng giải: Ta sẽ sử dụng tính chất của hai đường thẳng song song để chuyển đổi các góc bằng nhau ở đỉnh $A$ xuống các góc ở đáy $B$ và $C$

Giải bài 9.34 Trang 83 Toán 7 Kết nối tri thức Tập 2: 

Ta có hình minh họa như sau:

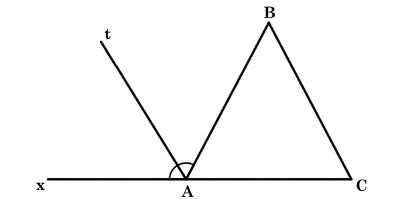
Gọi Ax là tia đối của tia AC.

Vì At là tia phân giác của $\widehat{BAx}$ nên $\widehat{xAt}=\widehat{tAB}$

Vì At // BC nên $\widehat{tAB}=\widehat{ABC}$ (2 góc so le trong).

Vì At // BC nên $\widehat{xAt}=\widehat{ACB}$ (2 góc đồng vị).

Mà $\widehat{xAt}=\widehat{tAB}$ suy ra: $\widehat{ABC}=\widehat{ACB}$

Xét ∆ABC có $\widehat{ABC}=\widehat{ACB}$

⇒ ∆ABC cân tại A (đpcm).