Giải bài 7 trang 38 Toán 10 tập 1 SGK Cánh Diều

Đề bài:

Cho hàm số y = f(x) có đồ thị như Hình 9.

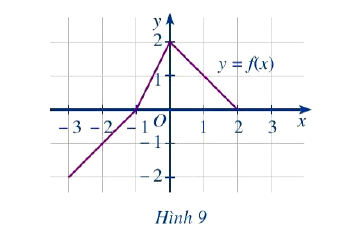
Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

Phân tích và Hướng dẫn giải:

Để xác định khoảng đồng biến và nghịch biến của hàm số $y = f(x)$ dựa vào đồ thị, ta xét chuyển động của đồ thị theo chiều từ trái sang phải (tức là theo chiều tăng của hoành độ $x$):

• Đồng biến: Đồ thị "đi lên". Điều này có nghĩa là khi $x$ tăng, giá trị $y = f(x)$ cũng tăng.

• Nghịch biến: Đồ thị "đi xuống". Điều này có nghĩa là khi $x$ tăng, giá trị $y = f(x)$ giảm.

Ta sẽ quan sát từng phần của đồ thị trong Hình 9 để đưa ra kết luận.

Lời giải chi tiết:

Từ đồ thị hàm số y = f(x) ở Hình 9, ta thấy:

- Đồ thị hàm số "đi lên" (theo chiều từ trái qua phải) trong các khoảng (–3; –1) và (–1; 0)

Nên hàm số đã cho đồng biến trên các khoảng (–3; –1) và (–1; 0). 

- Đồ thị hàm số "đi xuống" (theo chiều từ trái qua phải) trong khoảng (0; 2)

Nên hàm số đã cho nghịch biến trên khoảng (0; 2).