Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

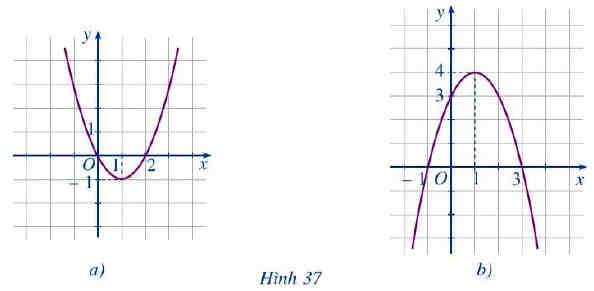
Quan sát đồ thị hàm số bậc hai y = ax² + bx + c ở Hình 37a và Hình 37b rồi nêu:

a) Dấu của hệ số a;

b) Tọa độ đỉnh và trục đối xứng;

c) Khoảng đồng biến;

d) Khoảng nghịch biến;

e) Khoảng giá trị x mà y > 0;

g) Khoảng giá trị x mà y ≤ 0. 

Phân tích và Hướng dẫn giải

Để phân tích đồ thị hàm số bậc hai y=ax²+bx+c, chúng ta cần dựa vào các đặc điểm sau:

• Dấu của hệ số a:

  • Nếu bề lõm của parabol hướng lên trên, $a>0$.

  • Nếu bề lõm của parabol hướng xuống dưới, $a<0$.

• Tọa độ đỉnh và trục đối xứng:

  • Đỉnh I(x; y) là điểm cao nhất hoặc thấp nhất của parabol.

  • Trục đối xứng là đường thẳng đứng đi qua đỉnh, có phương trình x=x_I​.

• Khoảng đồng biến/nghịch biến:

  • Nếu $a>0$, hàm số nghịch biến ở bên trái đỉnh và đồng biến ở bên phải đỉnh.

  • Nếu $a<0$, hàm số đồng biến ở bên trái đỉnh và nghịch biến ở bên phải đỉnh.

• Dấu của y:

  • $y>0$: Phần đồ thị nằm phía trên trục hoành.

  • $y\le 0$: Phần đồ thị nằm phía dưới hoặc cắt trục hoành.

Lời giải chi tiết:

* Từ đồ thị hình 37a) ta thấy:

a) Bề lõm của đồ thị hướng lên trên nên hệ số a > 0 hay hệ số a mang dấu "+".

b) Tọa độ đỉnh I(1; –1), trục đối xứng x = 1. 

c) Vì hệ số a > 0 nên hàm số đồng biến trên khoảng (1; + ∞).

d) Hàm số nghịch biến trên khoảng (– ∞; 1). 

e) Phần parabol nằm phía trên trục hoành tương ứng với các khoảng (–∞; 0) và (2; +∞) nên hàm số y > 0 trên các khoảng giá trị của x là (–∞; 0) ∪ (2; +∞).

g) Phần parabol phía dưới trục hoành tương ứng với khoảng (0; 2) nên hàm số y < 0 trên (0; 2). Vậy khoảng giá trị của x mà y ≤ 0 là đoạn [0; 2]. 

* Từ đồ thị hình 37b) ta thấy:

a) Bề lõm của đồ thị hướng xuống dưới nên a < 0 hay hệ số a mang dấu "–".

b) Tọa độ đỉnh I(1; 4), trục đối xứng x = 1. 

c) Vì hệ số a < 0 nên hàm số đồng biến trên khoảng (– ∞; 1).

d) Hàm số nghịch biến trên khoảng (1; +∞). 

e) Phần parabol nằm phía trên trục hoành tương ứng với khoảng (–1; 3) nên khoảng giá trị của x là (–1; 3) thì y > 0. 

g) Phần parabol nằm phía dưới trục hoành tương ứng với các khoảng (–∞; –1) và (3; +∞) nên khoảng giá trị của x để y ≤ 0 là (–∞; –1] ∪ [3; +∞).