Giải bài 3 trang 43 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Vẽ đồ thị của mỗi hàm số sau:

a) y = 2x² – 6x + 4 

b) y = –3x² – 6x – 3

Phương pháp vẽ đồ thị:

Để vẽ đồ thị của hàm số bậc hai y = ax^2 + bx + c, các em cần xác định các yếu tố sau:

1. Tọa độ đỉnh I: x_I = -\frac{b}{2a}, y_I = f(x_I).

2. Trục đối xứng: Đường thẳng x = -\frac{b}{2a}.

3. Bề lõm: Đồ thị có bề lõm hướng lên trên nếu a > 0, và hướng xuống dưới nếu a < 0.

4. Các điểm đặc biệt:

   • Giao điểm với trục tung: Đặt x = 0 để tìm y = c.

   • Giao điểm với trục hoành: Đặt y = 0 để giải phương trình ax^2 + bx + c = 0.

5. Vẽ đồ thị: Dựa vào các điểm đã tìm được, vẽ một đường parabol mượt mà đi qua các điểm đó.

Lời giải chi tiết:

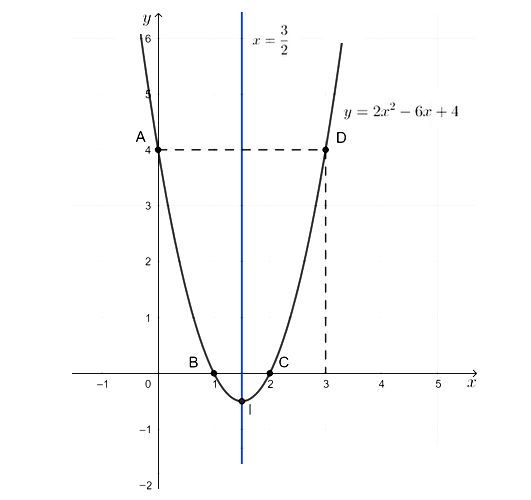
a) y = 2x² – 6x + 4

Ta có: a = 2, b = – 6, c = 4, ∆ = (– 6)² – 4 . 2 . 4 = 4. 

- Tọa độ đỉnh 

- Trục đối xứng 

- Giao điểm của parabol với trục tung là A(0; 4). 

- Giao điểm của parabol với trục hoành là B(1; 0) và C(2; 0). 

- Điểm đối xứng với điểm A(0; 4) qua trục đối xứng là D(3; 4). 

- Do a > 0 nên đồ thị có bề lõm hướng lên trên. 

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = 2x² – 6x + 4 như hình sau:

b) y = – 3x² – 6x – 3 

Ta có: a = –3, b = –6, c = –3,

∆ = (–6)² – 4 . (–3) . (– 3) = 0.

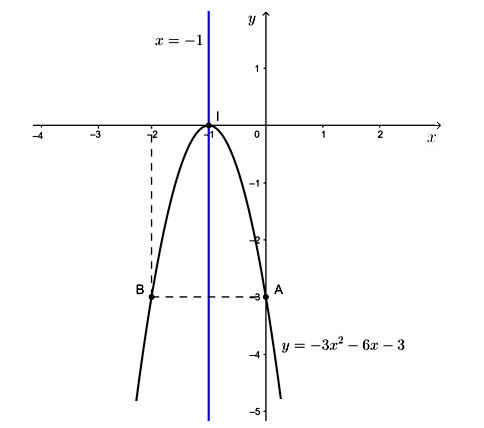
- Tọa độ đỉnh I(–1; 0).

- Trục đối xứng x = –1.

- Giao điểm của parabol với trục tung là A(0; –3). 

- Điểm đối xứng của A(0; –3) qua trục đối xứng x = –1 là điểm B(–2; –3). 

- Giao điểm của parabol với trục hoành chính là đỉnh I.

- Do a < 0 nên bề lõm của đồ thị hướng xuống. 

Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = –3x² – 6x – 3 như hình sau: