Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

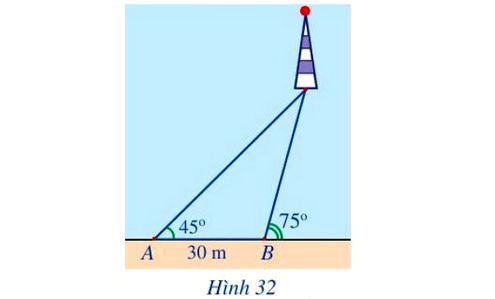
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°.

Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Phân tích và Phương pháp giải:

Bài toán yêu cầu tính khoảng cách từ ngọn hải đăng đến bờ biển. Ta có thể mô hình hóa bài toán này bằng một tam giác $ABC$ và một đường cao $CH$.

• Bước 1: Xác định các yếu tố đã biết của tam giác $ABC$. Đề bài cho khoảng cách $AB=30$ m và hai góc ∠CAB=45∘, ∠CBA=75∘.

• Bước 2: Tìm góc còn lại của tam giác $ABC$ bằng cách sử dụng định lý tổng ba góc trong tam giác.

• Bước 3: Áp dụng định lý sin để tìm độ dài cạnh $CB$.

• Bước 4: Sử dụng tam giác vuông $CBH$ để tính độ dài đường cao $CH$, chính là khoảng cách từ ngọn hải đăng đến bờ biển.

Lời giải chi tiết:

Giả sử C là vị trí của ngọn hải đăng, kẻ CH vuông góc AB thì CH là khoảng cách giữa ngọn hải đăng và bờ như hình sau:

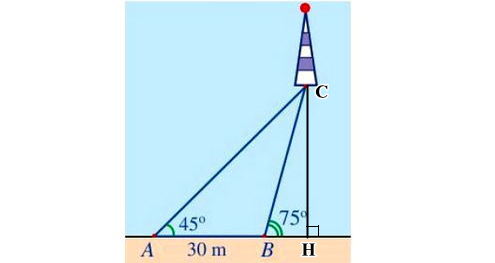
Ta có:  là góc ngoài tại đỉnh B của ΔABC. 

Nên:

Áp dụng định lí sin trong ΔABC ta có:

Xét ΔCBH vuông tại H nên: 

Vậy ngọn hải đăng cách bờ biển khoảng 41 m.