Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

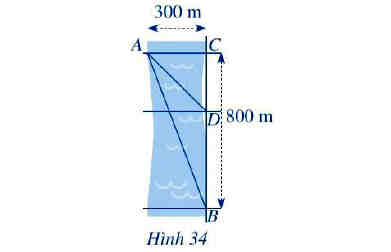
Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34.

Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, chúng ta sẽ thực hiện theo các bước sau:

1. Đổi đơn vị: Chuyển đổi tất cả các đơn vị về cùng một hệ (ví dụ: km và giờ) để dễ tính toán.

2. Lập phương trình:

   • Gọi ẩn số là khoảng cách cần tìm (CD = x).

   • Biểu diễn quãng đường di chuyển (AD, DB) và thời gian tương ứng (t1​,t2​) theo x.

   • Lập phương trình dựa trên tổng thời gian đã cho.

3. Giải phương trình: Giải phương trình vừa lập để tìm giá trị của x.

Lời giải chi tiết bài 4 trang 59 Toán 10:

Đổi: 300 m = 0,3 km; 800 m = 0,8 km; 7,2 phút = 0,12 giờ. 

Gọi độ dài khoảng cách từ vị trí C đến D là x (km, x > 0).

Khi đó ta có: AC = 0,3 km; CD = x km; BC = 0,8 km; DB = BC – CD = 0,8 – x (km). 

Lại có tam giác ACD vuông tại C, áp dụng định lý Pythagore ta có: 

AD² = AC² + CD² = (0,3)² + x² = 0,09 + x² 

Vì vậy, khoảng cách từ vị trí A đến vị trí D là km, mà vận tốc chèo thuyền là 6 km/h và vận tốc dòng nước không đáng kể nên thời gian người đó chèo thuyền từ vị trí A đến vị trí D là:

  (giờ). 

Quãng đường từ vị trí D đến vị trí B là 0,8 – x (km) và vận tốc chạy bộ là 10 km/h nên thời gian người đó chạy bộ từ vị trí D đến vị trí B là:

 (giờ). 

Tổng thời gian người đó chèo thuyền là  t₁ + t₂ = t = 0,12 (giờ). 

 (*)

Bình phương cả hai vế của (*) ta được: 25.(0,09 + x²) = (3x + 1,2)² 

⇔ 2,25 + 25x² = 9x² + 7,2x + 1,44

⇔ 16x² – 7,2x + 0,81 = 0 

⇔ x = 0,225 (thỏa điều kiện x > 0)

⇒ x = 0,225 km = 225 m.

Vậy khoảng cách từ vị trí C đến D là 225 m.