Giải bài 2 trang 48 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

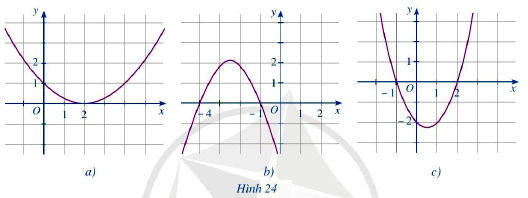
Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai f(x) với đồ thị được cho ở mỗi Hình 24a, 24b, 24c.

Phân tích và Hướng dẫn giải:

Để tìm nghiệm và lập bảng xét dấu của tam thức $f(x)$, ta thực hiện các bước sau:

1. Tìm nghiệm: Quan sát hoành độ của các điểm giao nhau giữa parabol và trục hoành (trục $Ox$).

2. Xét dấu:

   • $f(x) > 0$ khi parabol nằm hoàn toàn phía trên trục $Ox$.

   • $f(x) < 0$ khi parabol nằm hoàn toàn phía dưới trục $Ox$.

   • $f(x) = 0$ tại các nghiệm đã tìm được.

3. Lập bảng xét dấu: Sắp xếp các nghiệm theo thứ tự tăng dần và điền dấu ($+$, $-$, $0$) vào các khoảng tương ứng.

Lời giải chi tiết:

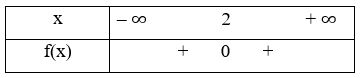
a) Từ hình 24a, ta thấy đồ thị cắt trục hoành tại một điểm có tọa độ (2; 0). 

Nên nghiệm của tam thức bậc hai f(x) là x = 2. 

Phần parabol nằm hoàn toàn phía trên trục hoành trừ điểm có hoành độ x = 2, nên ta có bảng xét dấu tam thức f(x) là: 

b) Từ hình 24b, ta thấy đồ thị cắt trục hoành tại 2 điểm phân biệt có tọa độ là (–4; 0) và (–1; 0).

Nên tam thức bậc hai f(x) có hai nghiệm phân biệt là x₁ = –4 và x₂ = –1.

Trên các khoảng (–∞; –4) và (–1; +∞), phần parabol nằm hoàn toàn phía dưới trục hoành nên f(x) < 0. 

Trên khoảng (–4; –1), phần parabol nằm phía trên trục hoành nên f(x) > 0.

Ta có bảng xét dấu tam thức f(x) sau: 

c) Từ hình 24c, ta thấy đồ thị cắt trục hoành tại hai điêm phân biệt có tọa độ (–1; 0) và (2; 0). 

Nên tam thức bậc hai f(x) có hai nghiệm phân biệt x₁ = –1 và x₂ = 2. 

Trên các khoảng (–∞; –1) và (2; +∞), phần parabol nằm phía trên trục hoành nên f(x) > 0. 

Trên khoảng (–1; 2) phần parabol nằm phía dưới trục hoành nên f(x) < 0. 

 Ta có bảng xét dấu tam thức f(x) sau: