Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau:

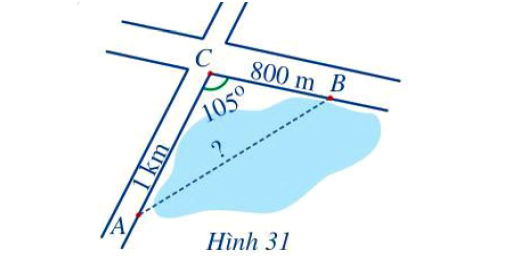
Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

Phân tích và Hướng dẫn giải:

Bài toán yêu cầu tính khoảng cách $AB$ khi biết các thông số trong tam giác $ABC$: $AC=1\text{ km}$, $CB=800\text{ m}$ và góc ∠ACB=105^∘. Đây chính xác là dạng bài toán sử dụng định lý côsin để tìm độ dài một cạnh khi biết độ dài hai cạnh còn lại và góc xen giữa.

• Bước 1: Đổi tất cả các đơn vị về cùng một hệ thống. Vì yêu cầu làm tròn đến hàng phần mười theo đơn vị mét, ta sẽ đổi $1\text{ km}$ thành $1000\text{ m}$.

• Bước 2: Áp dụng công thức định lý côsin: c²=a²+b²−2ab.cosC.

  Trong bài toán này, AB²=AC²+CB²−2⋅AC⋅CB⋅cos(∠ACB).

• Bước 3: Thay các giá trị đã biết vào công thức và tính toán.

• Bước 4: Lấy căn bậc hai của kết quả và làm tròn đến hàng phần mười.

Lời giải chi tiết:

Nối A với B, ba vị trí A, B, C tạo thành 3 đỉnh của tam giác ABC.

Ta có: 1 km = 1 000 m. 

Tam giác ABC có AC = 1 000 m, CB = 800 m và 

Áp dụng định lí côsin cho ΔABC ta có: 

AB² = AC² + CB² – 2 . AC . CB . cosACB 

= 1 000² + 800² – 2 . 1 000 . 800 . cos 105° ≈ 2 054 110,5 

⇒ AB ≈ 1 433,2 m. 

Vậy khoảng cách AB khoảng 1 433,2 m