Giải bài 2 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Bất phương trình bậc 2

Đề bài:

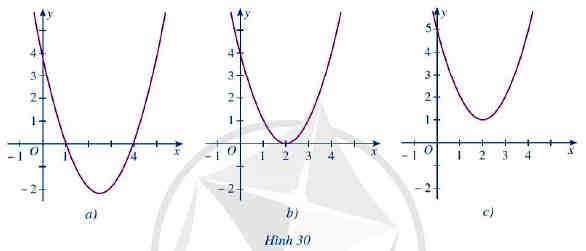
Dựa vào đồ thị hàm số bậc hai y = f(x) trong mỗi Hình 30a, 30b, 30c, hãy viết tập nghiệm của mỗi bất phương trình sau: f(x) > 0, f(x) < 0; f(x) ≥ 0; f(x) ≤ 0.

Phân tích và Hướng dẫn giải

Để giải các bất phương trình $f(x)>0$, $f(x)<0$, $f(x)\ge 0$, $f(x)\le 0$ dựa vào đồ thị, chúng ta cần xác định vị trí của đồ thị parabol so với trục hoành $Ox$.

• $f(x)>0$: Tìm các khoảng giá trị của $x$ mà phần đồ thị nằm hoàn toàn phía trên trục hoành.

• $f(x)<0$: Tìm các khoảng giá trị của $x$ mà phần đồ thị nằm hoàn toàn phía dưới trục hoành.

• $f(x)=0$: Tìm các giá trị của $x$ mà đồ thị cắt trục hoành. Các giá trị này chính là nghiệm của phương trình.

• $f(x)\ge 0$: Kết hợp các khoảng mà $f(x)>0$ và các điểm mà $f(x)=0$.

• $f(x)\le 0$: Kết hợp các khoảng mà $f(x)<0$ và các điểm mà $f(x)=0$.

Dựa vào quy tắc trên, ta sẽ phân tích từng đồ thị để tìm tập nghiệm.

Lời giải chi tiết bài 2 trang 54 Toán 10:

* Hình 30 a)

Từ đồ thị ta thấy: 

• f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x < 1 hoặc x > 4.

⇒ Tập nghiệm của bất phương trình f(x) > 0 là (–∞; 1) ∪ (4; +∞). 

Và tập nghiệm của bất phương trình f(x) ≥ 0 là (–∞; 1] ∪ [4; +∞). 

• f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, tương ứng với 1 < x < 4. 

⇒ Tập nghiệm của bất phương trình f(x) < 0 là (1; 4). 

Và tập nghiệm của bất phương trình f(x) ≤ 0 là [1; 4]. 

* Hình 30 b)

Từ đồ thị ta thấy:

• f(x) = 0 tại x = 2

• f(x) > 0 biểu diễn phần parabol y = f(x) nằm phía trên trục hoành, tương ứng với x ≠ 2.

⇒ Tập nghiệm của bất phương trình f(x) > 0 là R\{2}

Và tập nghiệm của bất phương trình f(x) ≥ 0 là R

• f(x) < 0 biểu diễn phần parabol y = f(x) nằm phía dưới trục hoành, mà phần đồ thị nằm phía trên trục hoành.

⇒ Bất phương trình f(x) < 0 vô nghiệm.

Và nghiệm của bất phương trình f(x) ≤ 0 là x = 2. 

* Hình 30 c)

Từ đồ thị ta thấy:

• Phần parabol nằm hoàn toàn phía trên trục hoành, vì vậy f(x) > 0 với mọi x ∈ R

Vậy tập nghiệm của bất phương trình f(x) > 0 là x ∈ R và các bất phương trình f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 vô nghiệm.