Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Cho tam giác ABC có AB = 12, AC = 15, BC = 20. Tính:

a) Số đo các góc A, B, C; 

b) Diện tích tam giác ABC. 

Phân tích và Phương pháp giải:

Bài toán cung cấp độ dài của ba cạnh trong tam giác $ABC$: $AB=12$, $AC=15$, $BC=20$. Chúng ta sẽ giải quyết bài toán theo các bước sau:

• Câu a: Sử dụng hệ quả của định lý côsin để tính số đo các góc $A,B,C$.

  Công thức tính $\cos$ của một góc khi biết ba cạnh là:

   

  

  

• Câu b: Sử dụng công thức Heron để tính diện tích tam giác khi biết ba cạnh.

  Công thức Heron được phát biểu như sau:

   với $p$ là nửa chu vi của tam giác, .

Lời giải chi tiết:

Ta có hình minh họa như sau:

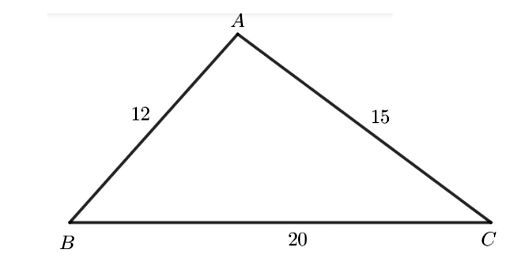
a) Số đo các góc A, B, C

Áp dụng hệ quả của định lí côsin ta có: 

b) Tính diện tích tam giác ABC

Diện tích tam giác ABC là: