Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là α = 35°;

khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là β = 75°;

khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so với mặt đất (làm tròn kết quả đến hàng đơn vị)?

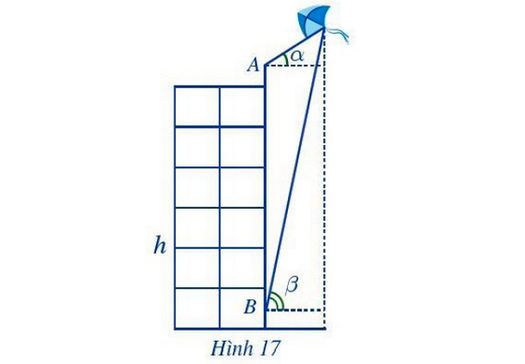
Phân tích và Hướng dẫn giải:

Ta đặt tên các điểm như trong hình (gọi$C$là vị trí chiếc diều, $A$là vị trí mắt bạn$A$trên đỉnh tòa nhà, $B$là vị trí mắt bạn$B$dưới chân tòa nhà,và$K$là vị trí mắt bạn$B$ngang bằng với mắt bạn$A$):

• Chiều cao tòa nhà ($T$): $20$m.

• Khoảng cách từ mắt đến các mốc: $1.5$m (đã được tính vào chiều cao$20$m của tòa nhà,hoặc$1.5 \text{m}$là khoảng cách từ đỉnh/chân tòa nhà đến mắt). Dựa vào hình vẽ và lời giải, ta giả sử $A$ và $B$ là vị trí mắt người quan sát.

• Góc nâng tại$A$: $\angle CAD = \alpha = 35^\circ$.(Gọi$AD$là phương nằm ngang).

• Góc nâng tại$B$: $\angle CBE = \beta = 75^\circ$.(Gọi$BE$là phương nằm ngang).

• Chiều cao của diều so với mặt đất ($CK$) bằng$CH + HK$.

Lời giải:

Ta đặt tên các điểm như trên hình sau:

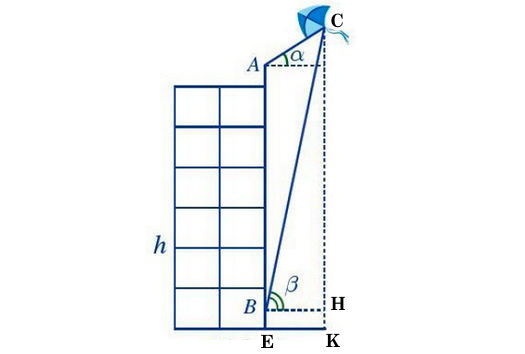
Ta có: AI là khoảng cách từ đỉnh của tòa nhà tới mắt bạn A nên AI = 1,5 m.

BE là khoảng cách từ mặt đất tới mắt của bạn B nên BE = 1,5 m.

Lại có: h = IB + BE ⇒ IB = h – BE = 20 – 1,5 = 18,5 (m).

Và AB = AI + IB = 1,5 + 18,5 = 20 (m)

Ta có: 

Theo định lí tổng ba góc trong ΔABC có:

Áp dụng định lí sin trong ΔABC ta có: 

Xét ΔCBH vuông tại H nên: 

⇒ CH = BC . sin β = 25,5 . sin 75° ≈ 24,6.

Lại có: HK = BE = 1,5 m.

Do đó CK = CH + HK = 24,6 + 1,5 = 26,1 (m). 

Vậy chiếc diều bay cao 26,1 m so với mặt đất.