Giải bài 5 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Hôm nay chúng ta sẽ cùng nhau giải chi tiết Bài 5 trang 61 sách giáo khoa Toán 10 tập 1, bộ sách Cánh Diều. Bài toán này giúp các em ôn tập cách vẽ đồ thị của hàm số bậc hai (y=ax2+bx+c), một kỹ năng cơ bản và quan trọng.
Đề bài:
Vẽ đồ thị của mỗi hàm số sau:
a) y = x2 – 3x – 4
b) y = x2 + 2x + 1
c) y = –x2 + 2x – 2.
Phân tích và Hướng dẫn vẽ đồ thị hàm số bậc hai:
Để vẽ đồ thị hàm số bậc hai (), ta cần xác định các yếu tố sau:
-
Dạng của parabol:
-
Nếu a > 0, parabol có bề lõm hướng lên trên.
-
Nếu a < 0, parabol có bề lõm hướng xuống dưới.
-
-
Tọa độ đỉnh I:
-
Hoành độ đỉnh:
.
-
Tung độ đỉnh:
.
-
-
Trục đối xứng:
-
Trục đối xứng là đường thẳng
.
-
-
Các giao điểm:
-
Giao điểm với trục tung: Cho
, ta tìm được
.
-
Giao điểm với trục hoành: Cho
, ta giải phương trình
.
-
-
Điểm phụ: Lấy thêm một vài điểm đối xứng qua trục đối xứng để đồ thị chính xác hơn.
Lời giải chi tiết:
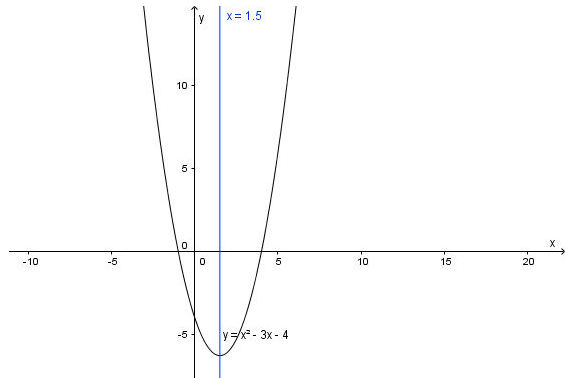
a) y = x2 – 3x – 4
Ta có: hệ số a = 1 > 0, b = –3, c = –4, ∆ = (–3)2 – 4.1.(–4) = 25 > 0.
- Parabol có bề lõm hướng lên trên.
- Tọa độ đỉnh
- Trục đối xứng
- Giao của parabol với trục tung là A(0; –4).
- Giao với trục hoành tại các điểm B(–1; 0) và C(4; 0).
- Điểm đối xứng với điểm A(0; – 4) qua trục đối xứng là điểm D(3; –4).
Vẽ đường cong đi qua các điểm trên ta được đồ thị của hàm số y = x2 – 3x – 4 như hình dưới.
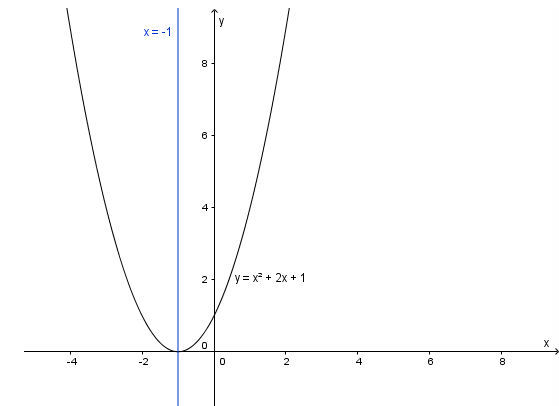
b) y = x2 + 2x + 1
Ta có hệ số a = 1 > 0, b = 2, c = 1, ∆ = 22 – 4 . 1 . 1 = 0.
- Parabol có bề lõm hướng lên trên.
- Tọa độ đỉnh I(– 1; 0).
- Trục đối xứng x = – 1.
- Giao của parabol với trục tung A(0; 1).
- Giao của parabol với trục hoành chính là đỉnh I(– 1; 0).
- Điểm đối xứng với điểm A(0; 1) qua trục đối xứng x = – 1 là điểm B(– 2; 1).
Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x2 + 2x + 1 như hình dưới.
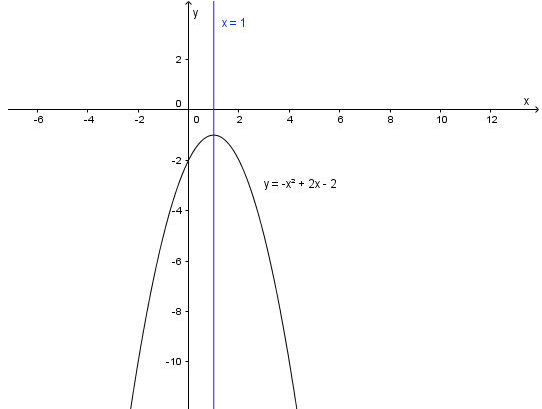
c) y = –x2 + 2x – 2.
y = – x2 + 2x – 2
Ta có hệ số a = – 1 < 0, b = 2, c = – 2 và ∆ = 22 – 4 . (– 1) . (– 2) = – 4.
- Đồ thị hàm số có bề lõm hướng xuống dưới.
- Tọa độ đỉnh I(1; – 1).
- Trục đối xứng x = 1.
- Giao của parabol với trục tung là A(0; – 2). Điểm đối xứng với A qua trục đối xứng x = 1 là B(2; – 2).
- Parabol không cắt trục hoành.
- Lấy điểm C(3; –5) thuộc đồ thị hàm số, ta có điểm đối xứng với điểm C qua trục x = 1 là điểm D(– 1; –5).
Vẽ đồ thị đi qua các điểm trên ta được đồ thị hàm số y = –x2 + 2x – 2 như hình vẽ dưới.
Qua bài tập này, các em đã rèn luyện được kỹ năng vẽ đồ thị hàm số bậc hai bằng cách xác định các yếu tố quan trọng như đỉnh, trục đối xứng và các giao điểm. Nắm vững các bước giải này sẽ giúp các em tự tin hơn khi làm bài tập về hàm số.
• Xem thêm:
Bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều: Tìm tập xác định của mỗi hàm số sau:...
Bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều: Giải các bất phương trình sau: a) 2x2 + 3x + 1 ≥ 0;...
Bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều: Giải các phương trình sau:...
Đánh giá & nhận xét
-
 Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 77 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 8 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 71 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 71 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 8 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 7 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 61 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 60 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Giải bất phương trình
Giải bài 3 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Giải bất phương trình
-
 Giải bài 2 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Bất phương trình bậc 2
Giải bài 2 trang 54 Toán 10 Tập 1 SGK Cánh Diều: Bất phương trình bậc 2
-
 Giải bài 1 trang 54 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 54 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 5 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 4 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 4 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 3 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 3 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 2 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 2 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 1 trang 48 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 1 trang 48 Toán 10 Tập 1 SGK Cánh Diều
-
 Giải bài 6 trang 43 Toán 10 Tập 1 SGK Cánh Diều
Giải bài 6 trang 43 Toán 10 Tập 1 SGK Cánh Diều


















































