Giải bài 2 trang 77 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Cho tam giác ABC có AB = 5, BC = 7,  Tính độ dài cạnh AC.

Phân tích và Phương pháp giải:

Bài toán cho tam giác $ABC$ với độ dài hai cạnh $AB=5$, $BC=7$ và số đo góc A^=120∘. Yêu cầu là tính độ dài cạnh $AC$. Để giải bài toán này, các em có thể áp dụng ngay định lý côsin. Mặc dù có thể sử dụng định lý sin như trong lời giải bạn cung cấp, nhưng cách đó sẽ phức tạp hơn và dễ dẫn đến sai số do phải làm tròn góc.

Định lý côsin phát biểu rằng:

a²=b²+c²−2bc.cosA

b²=a²+c²−2ac.cosB

c²=a²+b²−2ab.cosC

Trong bài toán này, chúng ta cần tìm cạnh $AC$, tương ứng với $b$.

Ta sẽ sử dụng công thức: BC²=AB²+AC²−2⋅AB⋅AC⋅cosA

Thay các giá trị đã biết vào và giải phương trình để tìm $AC$.

Lời giải chi tiết:

Ta có hình minh họa như sau:

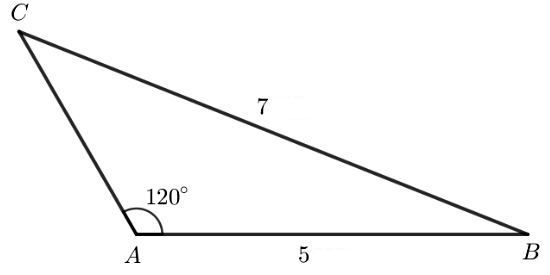
Áp dụng định lí sin vào ΔABC có:

Suy ra:

Mặt khác, theo định lí tổng ba góc trong ΔABC, ta có:

Áp dụng định lí côsin trong tam giác ABC ta có: 

AC² = AB² + BC² – 2 . AB . AC . cos B

= 5² + 7² – 2 . 5 . 7 . cos 21,8° ≈ 9

⇒ AC ≈ 3