Giải bài 6 trang 71 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí A đến vị trí C và tiến hành đo các góc BAC, BCA. Biết AC = 25 m, ,  (Hình 16). Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

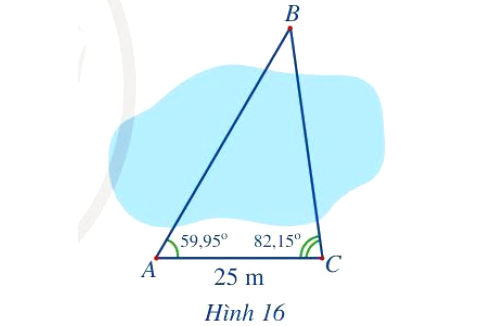
Phân tích và Hướng dẫn giải:

Ba vị trí $A, B, C$ tạo thành tam giác $ABC$. Ta có các thông số:

• Cạnh $b = AC = 25$ m.

• Góc $\angle A = 59.95^\circ$.

• Góc $\angle C = 82.15^\circ$.

Chúng ta cần tìm độ dài cạnh $AB$ (tức là $c$).

1. Tính góc $\angle B$: Sử dụng định lý tổng ba góc trong tam giác: $\angle B = 180^\circ - (\angle A + \angle C)$.

2. Tính cạnh AB: Áp dụng Định lý sin cho cặp cạnh-góc đối diện đã biết (AC;∠B) và cặp cần tìm (AB;∠C):

   $$\frac{AC}{\sin B} = \frac{AB}{\sin C}$$

   Từ đó, rút ra công thức tính AB.

Lời giải chi tiết:

Các vị trí A, B, C tạo thành 3 đỉnh của một tam giác. 

Theo định lý tổng ba góc trong một tam giác, ta có:

Áp dụng định lí sin trong tam giác ABC ta có:

Vậy khoảng cách từ vị trí A đến vị trí B khoảng 40 m.