Hotline 0936685849

Giải bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều

10:16:1806/08/2023

Hôm nay chúng ta sẽ cùng giải chi tiết Bài 3 trang 59 sách giáo khoa Toán 10 tập 1, bộ sách Cánh Diều. Bài toán này là một ứng dụng thực tế của định lý Pythagore và các hệ thức lượng trong tam giác vuông. Việc giải bài toán này không chỉ giúp bạn ôn tập kiến thức hình học mà còn rèn luyện kỹ năng vận dụng vào các tình huống thực tế.

Đề bài:

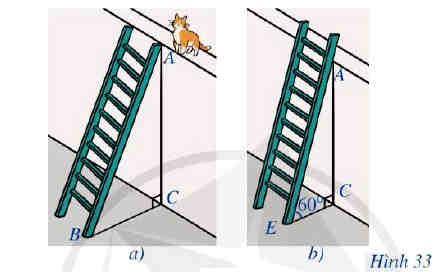
Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng và mép trên bức tường (Hình 33a).

Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc 60° (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Bài 3 trang 59 Toán 10 Tập 1 SGK Cánh Diều

Phân tích và Hướng dẫn giải

Để giải bài toán này, chúng ta sẽ sử dụng các kiến thức đã học về tam giác vuông. Cụ thể, bài toán yêu cầu tìm chiều cao của bức tường dựa trên các dữ kiện liên quan đến một chiếc thang. Ta có thể tóm tắt các bước giải như sau:

Bước 1: Đặt ẩn cho chiều cao của bức tường. Từ đó, biểu diễn chiều dài của chiếc thang và các đoạn thẳng khác theo ẩn này.
Bước 2: Áp dụng định lý Pythagore cho tam giác vuông ở Hình 33a để thiết lập một mối liên hệ giữa chiều cao của bức tường, chiều dài của thang và khoảng cách từ chân thang đến chân tường.
Bước 3: Sử dụng hệ thức lượng trong tam giác vuông ở Hình 33b. Cụ thể, ta sẽ sử dụng hàm $cos$ (cosin) để liên kết góc $6 0^{\circ}$ với các cạnh của tam giác vuông mới.
Bước 4: Lập phương trình và giải để tìm ra giá trị của ẩn.
Bước 5: Đối chiếu kết quả với điều kiện của bài toán và làm tròn kết quả đến hàng phần mười.

Lời giải chi tiết:

Gọi chiều cao của bức tường là x (mét) (x > 0).

Vì chiếc thang cao hơn tường 1 m nên chiều cao của chiếc thang là x + 1 (m).

Khi đó quan sát Hình 33a ta thấy: AC = x, AB = x + 1, tam giác ABC vuông tại C,

Áp dụng định lý Pythagore ta có: AB² = AC² + BC²

⇒ BC² = AB² – AC² = (x + 1)² – x² = 2x + 1

$\dpi{100} \small \Rightarrow BC=\sqrt{2x+1}\: \: (m)$

Ở hình 33b, ta thấy chiều cao bức tường không thay đổi nên DG = x (m).

Khi bác Nam dịch chuyển chân thang vào gần tường thêm 0,5 m thì: GE = BC – 0,5.

$\dpi{100} \small \Rightarrow GE=\sqrt{2x+1}-0,5\: \: (m)$

Mặt khác, ΔDGE vuông tại G nên ta có: $\small tan\widehat{DEG}=\frac{DG}{GE}$

Mà $\small \widehat{DEG}=60^0;\: \: DG=x;\: \: GE=\sqrt{2x+1}-0,5$

$\small \Rightarrow \frac{x}{\sqrt{2x+1}-0,5}=tan60^0=\sqrt{3}$

$\small \Rightarrow x=\sqrt{3}\left ( \sqrt{2x+1}-0,5 \right )$

$\dpi{100} \small\Leftrightarrow x= \sqrt{3(2x+1)}-\frac{\sqrt{3}}{2}$

$\dpi{100} \small\Leftrightarrow \sqrt{3(2x+1)}=x+\frac{\sqrt{3}}{2}$ (*)

Bình phương hai vế của (*) ta được: $3 (2 x + 1) = {(x + \frac{\sqrt{3}}{2})}^{2}$

$\small 3(2x+1)=\left ( x+\frac{\sqrt{3}}{2} \right )^2$

$\small \Leftrightarrow 6x+3=x^2+\sqrt{3}x+\frac{3}{4}$

$\dpi{100} \small \Leftrightarrow x^2+(\sqrt{3}-6)x-\frac{9}{4}=0$

$\small \Leftrightarrow \left \[\begin{matrix} x=\frac{6-\sqrt{3}+\sqrt{48-12\sqrt{3}}}{2}\approx 4,7\\ \\ x=\frac{6-\sqrt{3}-\sqrt{48-12\sqrt{3}}}{2}\approx -0,5 \end{matrix} \right.$

Vì x > 0 nên x ≈ 4,7 là giá trị thỏa mãn.

Vậy bức tường cao khoảng 4,7 m.

Bài toán đã được giải quyết bằng cách kết hợp định lý Pythagore và các hệ thức lượng trong tam giác vuông. Đây là một ví dụ điển hình cho thấy sự ứng dụng của toán học vào các bài toán thực tế.

• Xem thêm:

Bài 1 trang 58 Toán 10 Tập 1 SGK Cánh Diều: Giải các phương trình sau:...

Bài 2 trang 59 Toán 10 Tập 1 SGK Cánh Diều: Giải các phương trình sau:...

Bài 4 trang 59 Toán 10 Tập 1 SGK Cánh Diều: Một người đứng ở điểm A trên bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B...

Bài 5 trang 59 Toán 10 Tập 1 SGK Cánh Diều: Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho...