Bài 7.44 trang 46 Toán 7 Tập 2 Kết nối tri thức

Bài 7.44 Trang 46 Toán 7 Kết nối tri thức Tập 2: 

Cho đa thức A = x⁴ + x³ - 2x - 2.

a) Tìm đa thức B sao cho A + B = x³ + 3x + 1.

b) Tìm đa thức C sao cho A - C = x⁵.

c) Tìm đa thức D, biết rằng D = (2x² - 3) . A.

d) Tìm đa thức P sao cho A = (x + 1) . P.

e) Có hay không một đa thức Q sao cho Q = (x² + 1) . Q?

Phương Pháp Giải

1. Cộng/Trừ đa thức: Sử dụng quy tắc chuyển vế và nhóm các hạng tử đồng dạng.

2. Nhân đa thức: Áp dụng quy tắc nhân đa thức với đa thức.

3. Chia đa thức: Sử dụng thuật toán chia đa thức một biến đã sắp xếp. Nếu phép chia có dư khác 0 thì không tồn tại đa thức thương thỏa mãn yêu cầu.

Giải bài 7.44 Trang 46 Toán 7 Kết nối tri thức Tập 2: 

a) A + B = x³ + 3x + 1

B = x³ + 3x + 1 - A

B = x³ + 3x + 1 - (x⁴ + x³ - 2x - 2)

B = x³ + 3x + 1 - x⁴ - x³ + 2x + 2

B = -x⁴ + (x³ - x³) + (3x + 2x) + (1 + 2)

B = -x⁴ + 5x + 3

Vậy B = -x⁴ + 5x + 3.

b) A - C = x⁵

C = A - x⁵

C = x⁴ + x³ - 2x - 2 - x⁵

C = -x⁵ + x⁴ + x³ - 2x - 2

Vậy C = -x⁵ + x⁴ + x³ - 2x - 2.

c) D = (2x² - 3) . A

D = (2x² - 3) . (x⁴ + x³ - 2x - 2)

D = 2x² . (x⁴ + x³ - 2x - 2) + (-3) . (x⁴ + x³ - 2x - 2)

D = 2x².x⁴ + 2x².x³ + 2x².(-2x) + 2x².(-2) + (-3)x⁴ + (-3)x³ + (-3).(-2x) + (-3).(-2)

D = 2x⁶ + 2x⁵ - 4x³ - 4x² - 3x⁴ - 3x³ + 6x + 6

D = 2x⁶ + 2x⁵ - 3x⁴ + (-4x³ - 3x³) - 4x² + 6x + 6

D = 2x⁶ + 2x⁵ - 3x⁴ + (-7x³) - 4x² + 6x + 6

D = 2x⁶ + 2x⁵ - 3x⁴ - 7x³ - 4x² + 6x + 6

Vậy D = 2x⁶ + 2x⁵ - 3x⁴ - 7x³ - 4x² + 6x + 6.

d) A = (x + 1) . P

P = A : (x + 1)

P = (x⁴ + x³ - 2x - 2) : (x + 1)

Thực hiện phép chia ta được:

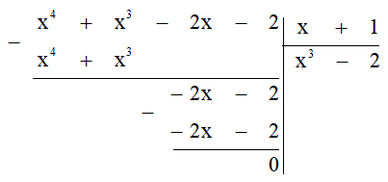
Vậy P = x³ - 2.

e) Thực hiện đặt phép chia đa thức A cho đa thức x² + 1 ta được:

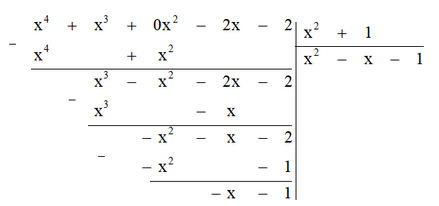
Ta thấy đa thức A chia cho đa thức x² + 1 dư -x - 1 nên không tồn tại đa thức Q sao cho

A = (x² + 1) . Q.

Qua bài tập 7.44, học sinh cần lưu ý các lỗi phổ biến sau:

• Nhầm dấu: Luôn đổi dấu tất cả hạng tử trong ngoặc khi có dấu trừ phía trước.

• Bỏ sót hạng tử: Khi chia đa thức, nếu đa thức bị chia thiếu bậc nào (ví dụ thiếu $x^2$ như ở câu d, e), hãy để trống hoặc viết thêm $0x^2$ để tránh đặt sai vị trí các cột dọc.

• Điều kiện tồn tại thương: Trong tập hợp các đa thức, $A = B \cdot Q$ chỉ xảy ra khi $A$ chia hết cho $B$.