Giải bài 5 trang 77 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

Tính độ dài cạnh AB trong mỗi trường hợp sau:

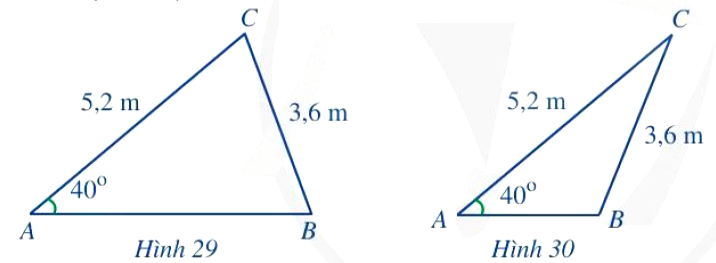
Phân tích và Phương pháp giải:

Bài toán yêu cầu tính độ dài cạnh $AB$ trong hai trường hợp được cho trong hình. Ta sẽ sử dụng các định lý đã học:

• Định lý sin:  

  Sử dụng định lý này để tìm các góc chưa biết.

• Định lý côsin: .

  Sử dụng định lý này để tính độ dài cạnh khi biết hai cạnh và góc xen giữa. Để giải quyết bài toán, chúng ta sẽ thực hiện các bước sau:

1. Sử dụng định lý sin để tìm số đo góc còn lại.

2. Sử dụng định lý tổng ba góc trong tam giác để tìm số đo góc còn lại.

3. Sử dụng định lý sin để tính độ dài cạnh $AB$.

Lời giải chi tiết:

* Với hình 29: Góc B nhọn. 

Áp dụng định lí sin trong ΔABC ta có:

Suy ra:  (do góc B nhọn)

Mặt khác, theo định lí tổng ba góc trong ΔABC, ta có:

Áp dụng định lí côsin trong tam giác ABC ta có: 

AB² = AC² + BC² – 2 . AC . BC . cos C

= (5,2)² + (3,6)² – 2 . 5,2 . 3,6 . cos 72° ≈ 28,43

⇒ AB ≈ 5,33 (m). 

* Với hình 30: Góc B tù. 

Khi đó: 

Mặt khác, theo định lí tổng ba góc trong ΔABC, ta có:

Áp dụng định lí côsin vào ΔABC có:

AB² = AC² + BC² – 2 . AC . BC . cosC

= (5,2)² + (3,6)² – 2 . 5,2 . 3,6 . cos 28° ≈ 6,94

⇒ AB ≈ 2,63 (m).