Giải bài 3 trang 12 Toán 11 tập 1 SGK Chân trời sáng tạo
Chào các em! Hôm nay chúng ta sẽ cùng giải chi tiết Bài 3 trang 12 trong sách giáo khoa Toán 11 tập 1, bộ sách Chân trời sáng tạo. Bài tập này giúp các em làm quen với việc biểu diễn góc lượng giác trên đường tròn lượng giác, một kỹ năng vô cùng quan trọng để hình dung và giải các bài toán lượng giác phức tạp.
Đề Bài 3 trang 12 Toán 11 tập 1:
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:
a)
b)
c) -7650
Phân tích và Hướng dẫn giải
Để biểu diễn một góc lượng giác trên đường tròn, các em cần thực hiện các bước sau:
-
Phân tích góc: Tách góc đã cho thành tổng của một số nguyên lần góc đầy đủ (2π hoặc 360∘) và một góc còn lại (α0). Công thức chung là α=α0+k⋅2π (với radian) hoặc α=α0+k⋅360∘ (với độ), trong đó α0 là góc chính cần biểu diễn và k là số vòng quay.
-
Xác định vị trí:
-
Vị trí ban đầu: Luôn bắt đầu từ điểm A(1;0) trên đường tròn.
-
Chiều quay: Nếu góc là số dương, quay ngược chiều kim đồng hồ. Nếu góc là số âm, quay cùng chiều kim đồng hồ.
-
Số vòng quay: Phần k⋅2π hoặc k⋅360∘ cho biết số vòng quay và chiều quay. Sau khi quay đủ số vòng, điểm cuối cùng sẽ quay về vị trí của góc α0.
-
-
Biểu diễn: Dựa vào vị trí của góc α0, ta xác định được điểm cuối cùng của góc lượng giác trên đường tròn.
Lời giải chi tiết:
a) Ta có:
Vì vậy điểm biếu diễn góc lượng giác có số đo là điểm nằm trên phần đường tròn lượng giác thuộc góc phần tư thứ I sao cho
hay
Biểu diễn góc này trên đường tròn lượng giác như sau:
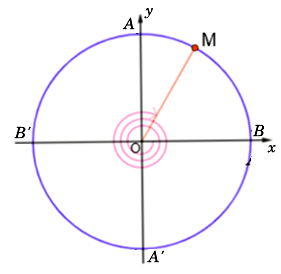
b) Ta có:
Biểu diễn góc này trên đường tròn lượng giác như sau:
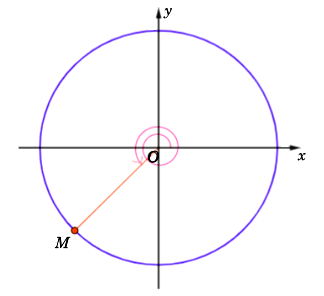
c) Ta có: – 765° = (– 2).360° – 45°
Biểu diễn góc này trên đường tròn lượng giác như sau:
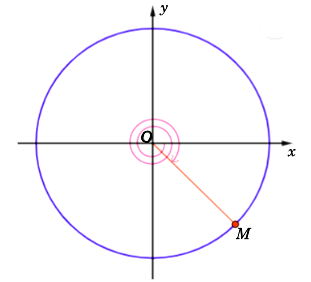
Qua bài tập này, các em đã học được cách đơn giản hóa một góc lượng giác về góc chính của nó để xác định vị trí trên đường tròn. Kỹ năng này sẽ giúp các em giải quyết các bài toán về hàm số lượng giác một cách trực quan và chính xác hơn.
• Xem thêm:
Bài 1 trang 12 Toán 11 tập 1 SGK Chân trời sáng tạo: Đổi số đo của các góc dưới đây sang radian:...
Bài 2 trang 12 Toán 11 tập 1 SGK Chân trời sáng tạo: Đổi số đo của các góc sau đây sang độ:...
Đánh giá & nhận xét
-
 Giải bài 4 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 140 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 140 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 134 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 134 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo: Hình vuông nội tiếp đường tròn
Giải bài 3 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo: Hình vuông nội tiếp đường tròn
-
 Giải bài 2 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 119 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 119 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 111 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 111 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 105 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 105 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo


















































