Giải bài 5 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho hình chóp S.ABCD có đáy là hình bình hành, AC và BD cắt nhau tại O. Gọi I là trung điểm của SO. Mặt phẳng (ICD) cắt SA, SB lần lượt tại M, N.

a) Hãy nói cách xác định hai điểm M và N. Cho AB = a. Tính MN theo a

b) Trong mặt phẳng (CDMN), gọi K là giao điểm của CN và DM. Chứng minh SK//BC//AD

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, bạn cần thực hiện theo các bước sau:

• Phần a:

  1. Xác định vị trí $M$ và $N$: Tìm giao điểm của đường thẳng và mặt phẳng bằng phương pháp giao tuyến phụ. Cụ thể, để tìm $M$, ta xét đường thẳng $CI$ và mặt phẳng $(SAB)$. Tương tự cho $N$.

  2. Tính $MN$: Sử dụng định lí Menelaus cho tam giác $SAB$ để tìm tỉ lệ các đoạn thẳng. Từ đó, bạn có thể tính được độ dài $MN$ dựa vào $AB$.

• Phần b:

  1. Xác định giao tuyến $SK$: Chứng minh $S$ và $K$ là hai điểm chung của mặt phẳng $(SAD)$ và $(SBC)$. Giao tuyến sẽ là đường thẳng $SK$.

  2. Chứng minh $SK//BC//AD$: Dựa vào tính chất của hình bình hành và giao tuyến của hai mặt phẳng song song, bạn có thể chứng minh được mối quan hệ song song giữa $SK$, $BC$ và $AD$.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

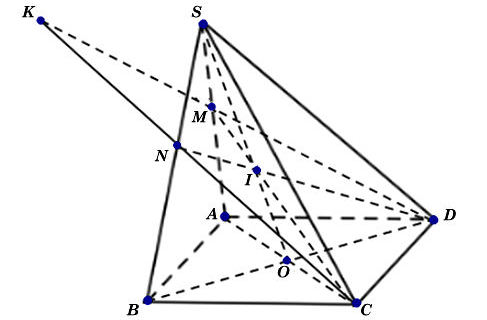
a) Trong mặt phẳng (SAC), gọi M là giao của CI và SA.

 CI ⊂ (ICD) nên M ∈ (ICD)

Trong mặt phẳng (SBD), gọi N là giao của DI và SB.

 DI ⊂ (ICD) nên N ∈ (ICD)

Ta có MN là giao của của (ICD) và (SAB). Mà AB//CD nên MN//CD

Theo định lý Menelaus, trong tam giác SOA, ta có:

Ta có MN//AB nên 

b) Ta có:

 K ∈ CN mà CN ⊂ (SBC) nên K ∈ (SBC)

 K ∈ DM mà DM ⊂ (SAD) nên K ∈ (SAD)

Mặt khác: S và K là hai điểm chung của hai mặt phẳng (SAD) và (SBC)

nên SK là giao tuyến của hai mặt phẳng (SAD) và (SBC).

Mà AD//BC nên SK//BC//AD