Giải bài 4 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho hình hộp ABCD.A'B'C'D'. Gọi G₁ và G₂ lần lượt là trọng tâm của hai tam giác BDA' và B'D'C. Chứng minh G₁ và G₂ chia đoạn AC' thành ba phần bằng nhau.

Phân tích và Hướng dẫn giải:

Đề bài cho hình hộp ABCD.A'B'C'D'. G₁ và G₂ lần lượt là trọng tâm của hai tam giác BDA' và B'D'C. Yêu cầu là chứng minh G₁, G₂ chia đoạn AC' thành ba phần bằng nhau.

Để giải quyết bài toán, chúng ta sẽ sử dụng phương pháp vector. Mấu chốt của bài toán là biểu diễn các vector liên quan đến G₁, G₂ và AC' theo một gốc chung (chẳng hạn A), sau đó chứng minh tỉ lệ của chúng.

Các bước thực hiện:

1. Xác định vị trí của $G_1$ và $G_2$: Sử dụng công thức trọng tâm tam giác để biểu diễn vector $\vec{AG_1}$ và $\vec{AG_2}$.

2. Biểu diễn các vector theo vector cơ sở: Biểu diễn các vector trong công thức trọng tâm theo một hệ vector cơ sở (ví dụ: $\vec{AB}, \vec{AD}, \vec{AA'}$).

3. So sánh tỉ lệ: So sánh các vector $\vec{AG_1}$ và $\vec{AG_2}$ với vector $\vec{AC'}$ để chứng minh chúng chia đoạn AC' thành ba phần bằng nhau.

Lời giải chi tiết:

Ta có hình minh hoạ như sau: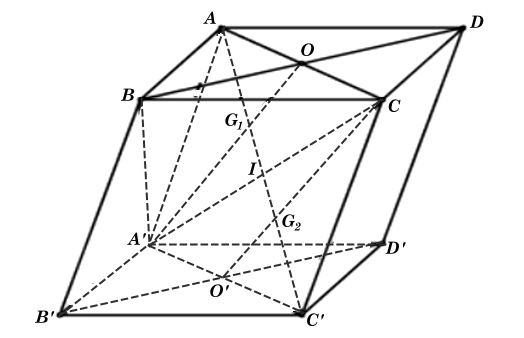

Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D', I là giao điểm của AC' và A'C

Do ACCA' là hình bình hành nên I là trung điểm của A'C

G1 là trọng tâm tam giác BDA' nên 

+ Tam giác AA'C có A'O là trung tuyến, 

nên G1 là trọng tâm của tam giác AA'C.

+ Mà I là trung điểm A'C nên G₁ ∈ AI và 

Mà  nên

Tương tự ta có C′G2=13AC′

Suy ra G₁, G₂ chia AC' thành 3 đoạn thẳng bằng nhau