Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I≠C), EG cắt AD tại H (H≠D)

a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD); (EFG) và (ACD)

b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm

Phân tích và Hướng dẫn giải:

Đề bài cho tứ diện ABCD và các điểm E, F, G trên các cạnh của nó. Bài toán có hai yêu cầu chính:

a) Tìm giao tuyến của các mặt phẳng: Để tìm giao tuyến của hai mặt phẳng, ta cần tìm hai điểm chung của chúng.

b) Chứng minh ba đường thẳng đồng quy: Để chứng minh ba đường thẳng cùng đi qua một điểm, ta có thể tìm giao điểm của hai trong ba đường thẳng đó, sau đó chứng minh giao điểm đó cũng nằm trên đường thẳng thứ ba.

Lời giải chi tiết:

a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD); (EFG) và (ACD)

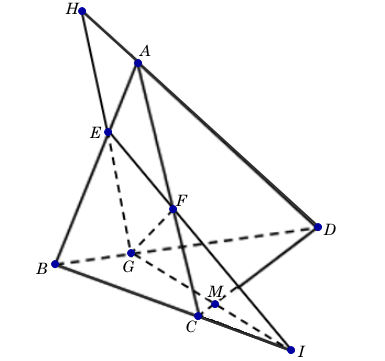
Ta có I và G là hai điểm chung của mặt phẳng (EFG) và (BCD)

nên GI là giao tuyến của (EFG) và (BCD)

Gọi M là giao điểm của GI và CD, khi đó

CD ⊂ (ACD) nên M ∈ (ACD)

Ta có M và F là điểm chung của mặt phẳng (EFG) và (ACD)

nên MF là giao tuyến của (EFG) và (ACD)

b) Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm

Ta có H ∈ AD mà AD⊂(ACD) nên H ∈ (ACD)

H ∈ EG mà EG ⊂ (EFG) nên H ∈ (EFG)

⇒ H là giao điểm của (EFG) và (ACD)

nên H nằm trên giao tuyến của (EFG) và (ACD): H ∈ FM.

Hay HF đi qua M.

Do đó, CD, IG, HF cùng đi qua điểm M.