Giải bài 4 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm của SD. Hai mặt phẳng (IAC) và (SBC) cắt nhau theo giao tuyến Cx. Chứng minh rằng Cx//SB.

Phân tích và Hướng dẫn giải:

Để giải bài toán này và chứng minh giao tuyến $Cx$ song song với $SB$, chúng ta cần áp dụng các phương pháp cơ bản của hình học không gian:

1. Tìm giao tuyến của hai mặt phẳng: Giao tuyến của hai mặt phẳng là đường thẳng chứa các điểm chung của chúng. Để tìm giao tuyến, ta cần tìm ít nhất hai điểm chung hoặc một điểm chung và sử dụng tính chất song song.

2. Sử dụng tính chất song song: Nếu hai đường thẳng song song thì chúng sẽ cùng song song với một đường thẳng khác, hoặc chúng tạo thành một hình bình hành.

3. Vận dụng các tính chất của hình chóp: Hình chóp có đáy là hình bình hành sẽ có các cặp cạnh đối song song và bằng nhau.

Cụ thể, ta sẽ tìm một tứ giác đặc biệt (hình bình hành) để suy ra mối quan hệ song song cần chứng minh.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

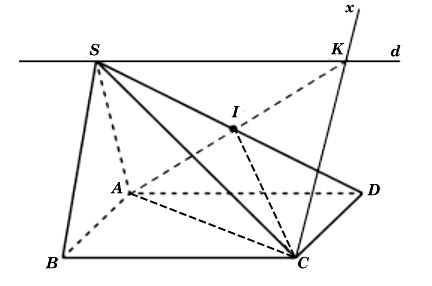
+ Mặt phẳng (SBC) và (SAD) giao nhau tại đường thẳng d đi qua S và song song với BC

Trong mặt phẳng (SAD), kéo dài AI cắt d tại K.

AI ⊂ (AIC) nên K ∈ (ACI)

+ Ta có C và K là 2 điểm chung của hai mặt phẳng (SBC) và (CIA) nên CK là giao tuyến của hai mặt phẳng (SBC) và (CIA)

+ Trong mặt phẳng (SADK) ta có AD//SK, I là trung điểm của SD nên AD = SK. Mà AB = BD.

Suy ra: SK = BC

+ Ta có SK // BC, SK = BC nên SBCK là hình bình hành.

Suy ra CK // SB.

Hay Cx // SB