Giải bài 4 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo

Đề bài:

Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây:

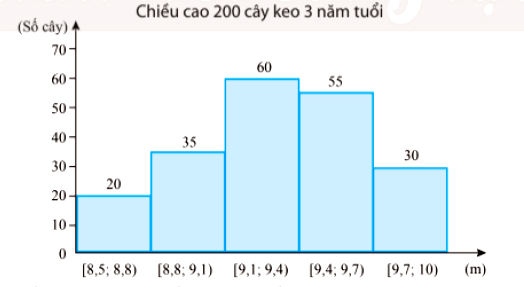
Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.

Phân tích và Hướng dẫn giải:

Đề bài cho bảng tần số ghép nhóm về chiều cao của 200 cây keo và yêu cầu ước lượng số trung bình cùng với mốt của mẫu số liệu.

Để giải quyết bài toán này, chúng ta sẽ thực hiện các bước sau:

1. Ước lượng số trung bình:

   • Tìm giá trị đại diện của mỗi nhóm bằng cách lấy trung bình cộng của hai đầu mút của nhóm.

   • Sử dụng công thức ước lượng giá trị trung bình: , với x_i​ là giá trị đại diện và n_i​ là tần số của nhóm thứ $i$.

2. Ước lượng mốt:

   • Xác định nhóm chứa mốt (nhóm có tần số lớn nhất).

   • Sử dụng công thức ước lượng mốt: , với $L$ là đầu mút trái của nhóm chứa mốt, nm​ là tần số của nhóm chứa mốt, nm−1​ và nm+1​ là tần số của nhóm trước và sau, $h$ là chiều rộng của nhóm.

Lời giải chi tiết:

Chiều cao của 200 cây keo được thống kê như bảng sau:

Chiều cao trung bình của 200 cây xấp xỉ bằng:

(8,65.20+8,95.35+9,25.60+9,55.55+9,85.30):200=9,31 (m)

Nhóm chứa mốt của mẫu số liệu là [9,1;9,4)

Do đó: u_m=9,1; n_m−1=35; n_m+1=55;

u_m+1−u_m=9,4−9,1=0,3

Mốt của mẫu số liệu trên là:

Thay số, ta được: